题目内容
两个长度相等、倾角都是α的斜面,一个是光滑的,另一个是粗糙的,物体从粗糙斜面顶端匀加速滑到底端所用时间,为从光滑斜面滑到底端所用时间的3倍.那么,物体在光滑斜面和粗糙斜面上,下滑的加速度之比为 ,物体与粗糙斜面间的动摩擦因数为 .
【答案】分析:物体沿着光滑斜面下滑时,受重力和支持力,根据牛顿第二定律列式求解加速度,再根据位移时间关系公式列式求解时间;物体沿着粗糙斜面下滑时,受重力和支持力和滑动摩擦力,再次根据牛顿第二定律列式求解加速度,并根据位移时间关系公式列式求解时间;最后联立求解即可.
解答:解:物体从光滑斜面滑下时,根据牛顿第二定律,有
mgsinα=ma ①
根据位移时间关系公式,有
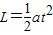 ②
②
物体从粗糙斜面滑下时,根据牛顿第二定律,有
mgsinα-μmgcosα=ma′③
根据位移时间关系公式,有
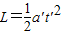 ④
④
根据题意
t′=3t ⑤
由①②③④⑤联立解得
a:a′=9:1
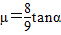
故答案为:9:1,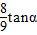 .
.
点评:本题是已知运动情况确定受力情况的问题,关键是先求解出加速度,然后再受力分析并根据牛顿第二定律列式求解.
解答:解:物体从光滑斜面滑下时,根据牛顿第二定律,有
mgsinα=ma ①
根据位移时间关系公式,有
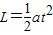 ②
②物体从粗糙斜面滑下时,根据牛顿第二定律,有
mgsinα-μmgcosα=ma′③
根据位移时间关系公式,有
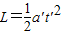 ④
④根据题意
t′=3t ⑤
由①②③④⑤联立解得
a:a′=9:1
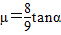
故答案为:9:1,
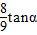 .
.点评:本题是已知运动情况确定受力情况的问题,关键是先求解出加速度,然后再受力分析并根据牛顿第二定律列式求解.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目