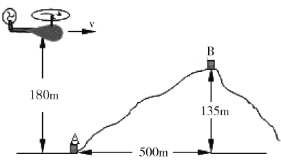
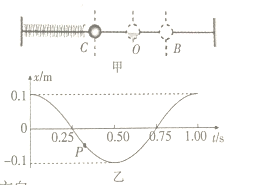
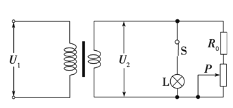
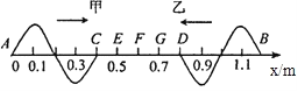题目内容
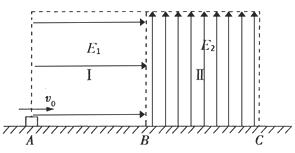
【题目】如图所示,在绝缘水平面上方,有两个边长d=0.2m的正方形区域I、Ⅱ,其中区域I中存在水平向右的大小E1=30N/C的匀强电场、区域Ⅱ中存在竖直向上的大小E2=150N/C的匀强电场。现有一可视为质点的质量m=0.3kg的滑块,以v0=1m/s的初速度从区域I边界上的A点进入电场,经过一段时间后,滑块从区域II边界上的D点离开电场(D点未画出),滑块的电荷量q=+0.1C,滑块与水平面间的动摩擦因数μ=0.75,重力加速度取g=10m/s2。
问:
(1)滑块进入区域II时的速度是多少?
(2)D点与A点的水平距离、竖直距离分别为多少?
(3)若仅改变区域Ⅱ中电场强度的大小,要使滑块从区域Ⅱ中的右边界离开电场,则区域Ⅱ中电场强度大小E的取值范围应为多少?
【答案】(1)vB=![]() m/s;(2)竖直距离yAD=0.2m,水平距离xAD
m/s;(2)竖直距离yAD=0.2m,水平距离xAD![]() m;(3)10N/C<E≤90N/C
m;(3)10N/C<E≤90N/C
【解析】
(1)滑块在区域I中运动时,设滑块的加速度![]() ,根据牛顿第二定律可得:
,根据牛顿第二定律可得:
![]()
设滑块运动到两电场区域的交界点B的速度为vB,则:
![]()
联立解得
vB=![]() m/s
m/s
(2)滑块在区域Ⅱ中做类平抛运动时,竖着向上的加速度![]() ,根据牛顿第二定律得:
,根据牛顿第二定律得:
![]()
解得
a2=40m/s2
假设滑块从区域Ⅱ的上边界离开电场区域,运动的时间为t0,根据类平抛运动的规律得,滑块在水平方向上做匀速运动,则
x1=vBt0
在竖直方向上做匀加速运动,则
![]()
联立解得
![]() <d
<d
因此假设成立;
A、D两点之间的竖直距离
yAD=d=0.2m
A、D两点之间的水平距离
xAD=d+![]() m
m
(3)滑块在区域Ⅱ中运动,刚好从右边界的最上端离开时,竖着向上的加速度![]() ,电场强度
,电场强度![]() ,根据类平抛运动的规律,水平方向上
,根据类平抛运动的规律,水平方向上
d=vBt
竖直方向上有
![]()
根据牛顿第二定律得
![]()
联立并代入数据解得
E3=90N/C
若滑块到达C点时速度刚好为0,电场强度![]() ,水平方向的加速度
,水平方向的加速度![]() ,由运动学规律得
,由运动学规律得
![]()
根据牛顿第二定律得
![]()
联立并代入数据解得
E4=10N/C
则区域B中的电场强度10N/C<E≤90N/C时,滑块从区域Ⅱ的右边界离开。