题目内容
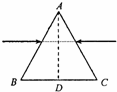 如图所示,一横截面为正三角形的棱镜ABC,其截面与纸面平行,AD垂直于BC.现有红光和紫光两细光束,从空气中沿与底边BC平行的方向相对射入棱镜,以下说法正确的是( )
如图所示,一横截面为正三角形的棱镜ABC,其截面与纸面平行,AD垂直于BC.现有红光和紫光两细光束,从空气中沿与底边BC平行的方向相对射入棱镜,以下说法正确的是( )分析:棱镜对红光的折射率小于对紫光的折射率,根据折射定律分析折射角的大小,确定两光束能否在AD线上交于同一点;光从空气进入棱镜,频率不变,光子的能量不变;根据折射定律分析偏折程度.
解答:解:A、棱镜对红光的折射率小于对紫光的折射率,根据折射定律n=
知,入射角相等时,红光的折射角大于紫光的折射角,而AD是BC边的中垂线,所以两光束不可能在镜内交于AD线上同一点.故A错误.
B、光从空气进入棱镜时,频率γ不变,光子的能量E=hγ,则知光子的能量不变,故B错误.
C、光在棱镜上的入射角与折射角的正弦之比等于棱镜对光的折射率,由于两光束的折射率不同,所以此比值不同,故C错误.
D、紫光的折射率较大,根据折射定律n=
知,紫光的折射角较小,偏折程度较大,故D正确.
故选D
| sini |
| sinr |
B、光从空气进入棱镜时,频率γ不变,光子的能量E=hγ,则知光子的能量不变,故B错误.
C、光在棱镜上的入射角与折射角的正弦之比等于棱镜对光的折射率,由于两光束的折射率不同,所以此比值不同,故C错误.
D、紫光的折射率较大,根据折射定律n=
| sini |
| sinr |
故选D
点评:本题关键要掌握红光与紫光折射率的大小关系,运用折射定律分析判断即可.

练习册系列答案
相关题目
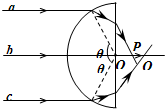 如图所示,一横截面为半圆形的玻璃柱体,三种颜色不同的可见光细光束a、b、c,垂直于直径从空气射向玻璃,b正好过圆心O,a、c从b 的两侧对称入射,已知θ=60°,该玻璃对a光的折射率为
如图所示,一横截面为半圆形的玻璃柱体,三种颜色不同的可见光细光束a、b、c,垂直于直径从空气射向玻璃,b正好过圆心O,a、c从b 的两侧对称入射,已知θ=60°,该玻璃对a光的折射率为| 3 |
| A、在玻璃中,c光的速度大于a光的速度 |
| B、玻璃对c 光的折射率大于对b 光的折射率 |
| C、在相同条件下进行双缝干涉实验,a 光的条纹间距比c 光大 |
| D、细光束a射出玻璃柱体后与细光束b的夹角为60° |
 如图所示,一横截面为直角三角形的三棱镜,∠B=90°,∠C=30°.一条与BC面成θ=30°角的光线射向AB面,经过BC边一次反射,再从AC边射出,且出射光线的折射角为60°.则这种材料的折射率为( )
如图所示,一横截面为直角三角形的三棱镜,∠B=90°,∠C=30°.一条与BC面成θ=30°角的光线射向AB面,经过BC边一次反射,再从AC边射出,且出射光线的折射角为60°.则这种材料的折射率为( ) (2011?浙江模拟)如图所示,一横截面为半圆形的玻璃柱体,三种颜色不同的可见光细光束a、b、c,垂直于直径从空气射向玻璃,b正好过圆心O,a、c从b 的两侧对称入射,已知θ=60°,该玻璃对a光的折射率为
(2011?浙江模拟)如图所示,一横截面为半圆形的玻璃柱体,三种颜色不同的可见光细光束a、b、c,垂直于直径从空气射向玻璃,b正好过圆心O,a、c从b 的两侧对称入射,已知θ=60°,该玻璃对a光的折射率为
 B.
B. C.
C. D.2
D.2