题目内容
5. 小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳突然断掉,球飞行水平距离d后落地,如图所示.已知握绳的手离地面高度为d,手与球之间的绳长为 $\frac{3}{4}$d,重力加速度为g,忽略手的运动半径和空气阻力.
小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动.当球某次运动到最低点时,绳突然断掉,球飞行水平距离d后落地,如图所示.已知握绳的手离地面高度为d,手与球之间的绳长为 $\frac{3}{4}$d,重力加速度为g,忽略手的运动半径和空气阻力.(1)求绳断时球的速度大小v1和球落地时的速度大小v2.
(2)问绳能承受的最大拉力多大?
分析 (1)绳断后小球做平抛运动,根据平抛运动的规律即可求解绳断时球的速度大小v1和球落地时的速度大小v2;
(2)设绳能承受的最大拉力大小为T,这也是球受到绳的最大拉力大小.根据向心力公式即可求解.
解答 解:(1)设绳断后球飞行时间为t,由平抛运动规律,竖直方向:
$\frac{1}{4}$d=$\frac{1}{2}$gt2
水平方向:
d=v1t
得:
v1=$\sqrt{2gd}$
由机械能守恒定律,有:
$\frac{1}{2}$mv22=$\frac{1}{2}$mv12+mg(d-$\frac{3}{4}$d)
解得:
v2=$\sqrt{\frac{5}{2}gd}$
(2)设绳能承受的最大拉力大小为T,这也是球受到绳的最大拉力大小,球做圆周运动的半径为:
R=$\frac{3}{4}$d
由圆周运动向心力公式,有:
T-mg=m$\frac{{v}_{1}^{2}}{R}$
解得:
T=$\frac{11}{3}$mg
答:(1)求绳断时球的速度大小 v1为$\sqrt{2gd}$,球落地时的速度大小 v2为$\sqrt{\frac{5}{2}gd}$;
(2)绳能承受的最大拉力为$\frac{11}{3}$mg.
点评 本题主要考查了圆周运动向心力公式及平抛运动的规律的应用,关键是记住基本公式,分圆周运动和平抛运动两个过程分析,基础题目.

练习册系列答案
相关题目
15. 如图所示,坐在雪橇上的人与雪橇的总质量为m,在与水平面成θ角的恒定拉力F作用下,沿水平地面向右移动了一段距离l.已知雪橇与地面间的动摩擦因数为μ,则雪橇受到的( )
如图所示,坐在雪橇上的人与雪橇的总质量为m,在与水平面成θ角的恒定拉力F作用下,沿水平地面向右移动了一段距离l.已知雪橇与地面间的动摩擦因数为μ,则雪橇受到的( )
 如图所示,坐在雪橇上的人与雪橇的总质量为m,在与水平面成θ角的恒定拉力F作用下,沿水平地面向右移动了一段距离l.已知雪橇与地面间的动摩擦因数为μ,则雪橇受到的( )
如图所示,坐在雪橇上的人与雪橇的总质量为m,在与水平面成θ角的恒定拉力F作用下,沿水平地面向右移动了一段距离l.已知雪橇与地面间的动摩擦因数为μ,则雪橇受到的( )| A. | 支持力做功为mgl | B. | 重力做功为mgl | ||
| C. | 拉力做功为Flcosθ | D. | 滑动摩擦力做功为μmgl |
16.下列说法正确的是( )
| A. | 地心说的代表人物是哥白尼,认为地球是宇宙的中心,其它星球都在绕地球运动 | |
| B. | 牛顿由于测出了万有引力常量而成为第一个计算出地球质量的人 | |
| C. | 地球和太阳的连线与火星和太阳的连线在相等时间内扫过的面积相等 | |
| D. | 由$\frac{GMm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r推出$\frac{{r}^{3}}{{T}^{2}}$=$\frac{GM}{4{π}^{2}}$=k,可知k值只与中心天体质量有关 |
13.以下关于自行车的许多部件的运动的描述正确的是( )
| A. | 前齿轮盘和后齿轮盘由于被同一条链条连接,所以线速度大小相等 | |
| B. | 后齿轮盘和脚踏板在同一个转轴上,所以角速度相同 | |
| C. | 如果前后轮半径相同则它们的线速度相同 | |
| D. | 如果前后轮半径不同则它们的线速度不同 |
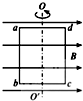 矩形线框abcd的边长分别为l1、l2,可绕它的一条对称轴OO′转动,线框电阻为R,转动角速度为ω.匀强磁场的磁感应强度为B,方向与OO′垂直,初位置时线圈平面与B平行,如图所示.
矩形线框abcd的边长分别为l1、l2,可绕它的一条对称轴OO′转动,线框电阻为R,转动角速度为ω.匀强磁场的磁感应强度为B,方向与OO′垂直,初位置时线圈平面与B平行,如图所示. 如图光滑轨道由半圆和一段竖直轨道构成,图中H=2R,其中R远大于轨道内径.比轨道内径略小的两小球A、B用轻绳连接,A在外力作用下静止于轨道右端口,B球静止在地面上,轻绳绷紧.现静止释放A小球,A落地后不反弹,此后B小球恰好可以到达轨道最高点.则A、B两小球的质量之比为( )
如图光滑轨道由半圆和一段竖直轨道构成,图中H=2R,其中R远大于轨道内径.比轨道内径略小的两小球A、B用轻绳连接,A在外力作用下静止于轨道右端口,B球静止在地面上,轻绳绷紧.现静止释放A小球,A落地后不反弹,此后B小球恰好可以到达轨道最高点.则A、B两小球的质量之比为( ) 如图所示,横截面为矩形ABCD的玻璃砖竖直放置在水平面面上,其厚度为d,AD面镀有水银,用一束与BC成45°角的细微光向下照射在BC面上,在水平面上出现两个光斑,距离$\frac{2}{3}\sqrt{3}$d,求玻璃砖的折射率.
如图所示,横截面为矩形ABCD的玻璃砖竖直放置在水平面面上,其厚度为d,AD面镀有水银,用一束与BC成45°角的细微光向下照射在BC面上,在水平面上出现两个光斑,距离$\frac{2}{3}\sqrt{3}$d,求玻璃砖的折射率. 某人乘坐出租车在平直公路上匀速行驶,如图为他乘车到达目的地时的车费发票.请你细心阅读车费发票,求出:
某人乘坐出租车在平直公路上匀速行驶,如图为他乘车到达目的地时的车费发票.请你细心阅读车费发票,求出: