题目内容
(1)两列相干波在同一水平面上传播,某时刻它们的波峰、波谷位置如图所示.图中M是波峰与波峰相遇点,是凸起最高的位置之一.回答下列问题:

①由图中时刻经T/4,质点M相对平衡位置的位移是
②在图中标出的M、N、O、P、Q几点中,振动增强的点是 ;振动减弱的点是 .
(2)如图所示,玻璃球的半径为R,折射率n=
,今有一束平行光沿直径AB方向照射在玻璃球上,试求离AB多远的入射光线最终射出后沿原方向返回.

①由图中时刻经T/4,质点M相对平衡位置的位移是
②在图中标出的M、N、O、P、Q几点中,振动增强的点是
(2)如图所示,玻璃球的半径为R,折射率n=
| 3 |
分析:(1)①M是波峰与波峰相遇点,振动加强,图中M点位于波峰,再经
,到达平衡位置,位移为零.②波峰与波谷相遇点,振动减弱.振动加强的区域内各点振动都加强.
(2)首先画出光路图,根据对称性得知θ1=2θ2 ,结合折射定律即可求出入射角θ1和折射角θ2.再根据几何知识求入射光线离AB的距离.
| T |
| 4 |
(2)首先画出光路图,根据对称性得知θ1=2θ2 ,结合折射定律即可求出入射角θ1和折射角θ2.再根据几何知识求入射光线离AB的距离.
解答: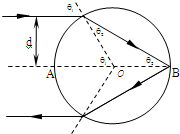 解:(1)①从该时刻经
解:(1)①从该时刻经
,质点M恰经过平衡位置,所以位移为0.
②该时刻.振动增强的点是:M、O、P、Q;振动减弱的点是:N.
(2)由光路图知,θ1=2θ2 ①
根据折射定律得:
=n ②
解①②式得
cosθ2=
,得θ2=30°,θ1=60°③
∵d=Rsinθ1 ④
∴d=
R ⑤
故答案为:
(1)①0;②M、O、P、Q;N.
(2)离AB
R的入射光线最终射出后沿原方向返回.
 解:(1)①从该时刻经
解:(1)①从该时刻经| T |
| 4 |
②该时刻.振动增强的点是:M、O、P、Q;振动减弱的点是:N.
(2)由光路图知,θ1=2θ2 ①
根据折射定律得:
| sinθ1 |
| sinθ2 |
解①②式得
cosθ2=
| ||
| 2 |
∵d=Rsinθ1 ④
∴d=
| ||
| 2 |
故答案为:
(1)①0;②M、O、P、Q;N.
(2)离AB
| ||
| 2 |
点评:本题考查了波动的干涉现象,抓住波峰与波峰相遇点,振动加强,波峰与波谷相遇点,振动减弱.
对于几何光学,正确画出光路图,要结合几何知识进行求解.
对于几何光学,正确画出光路图,要结合几何知识进行求解.

练习册系列答案
相关题目






 注入人体,
注入人体,
 D.液体表面层的分子比液体内部的分子有更大的分子势能
D.液体表面层的分子比液体内部的分子有更大的分子势能 D.超声波可以在真空中传播
D.超声波可以在真空中传播
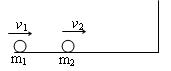
 ⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.
⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小. D.液体表面层的分子比液体内部的分子有更大的分子势能
D.液体表面层的分子比液体内部的分子有更大的分子势能 D.超声波可以在真空中传播
D.超声波可以在真空中传播
 注入人体,
注入人体, ⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.
⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.