题目内容
15. 如图所示,倾角θ=30°的绝缘光滑斜面向上,有一边界为矩形区域MNPQ磁场,边界MN为水平方向,MN与PQ之间距离为d=0.2m,以MN边界中点O为坐标原点沿斜面向上建立x坐标.已知磁场方向垂直于斜面向上,磁感应强度大小随坐标x位置变化,变化规律为B=$\sqrt{0.5-2.5x}$.现有n=10匝的正方形线圈abcd,其边长l=0.4m,总质量m=0.5kg、总电阻R=4Ω,ab边与MN 重合;在沿斜面向上的拉力F作用下,以恒定的速度v=1m/s,沿 x轴正向运动.g取10m/s2.
如图所示,倾角θ=30°的绝缘光滑斜面向上,有一边界为矩形区域MNPQ磁场,边界MN为水平方向,MN与PQ之间距离为d=0.2m,以MN边界中点O为坐标原点沿斜面向上建立x坐标.已知磁场方向垂直于斜面向上,磁感应强度大小随坐标x位置变化,变化规律为B=$\sqrt{0.5-2.5x}$.现有n=10匝的正方形线圈abcd,其边长l=0.4m,总质量m=0.5kg、总电阻R=4Ω,ab边与MN 重合;在沿斜面向上的拉力F作用下,以恒定的速度v=1m/s,沿 x轴正向运动.g取10m/s2.求:
(1)线圈ab边运动到x=0.1m位置时,线圈受到的安培力FA.
(2)线圈穿过磁场区域过程中拉力F 做的总功W.
分析 (1)根据法拉第电磁感应定律,结合闭合电路欧姆定律,及安培力表达式,即可求解;
(2)根据线圈经过磁场分三个阶段,结合动能定理,及几何关系,从而确定安培力与位移的关系,再结合图象,从而求得总功.
解答 解:(1)在x=0.1m处,磁感应强度B1=0.5T;
由电磁感应定律,则有:E=nBlv=2V;
根据闭合电路欧姆定律,则有:I1=$\frac{E}{R}$=$\frac{nBlv}{R}$=$\frac{2}{4}$=0.5A;
那么线圈受到的安培力大小FA=nBIl=$\frac{{n}^{2}{B}^{2}{l}^{2}v}{R}$=1N;
(2)线圈经过磁场区域分成三个阶段,第一阶段ab边在切割磁场,第二阶段线圈没有切割磁场,第三阶段线圈cd切割磁场
由动能定理,可得:W+WG+WA=0
h=(d+l)sinθ=0.3m
WG=mgh=-1.5J
由上可得,线圈受到安培力:FA=$\frac{{n}^{2}{B}^{2}{l}^{2}v}{R}$=2-10x(N)是变力
由FA-x图象可知,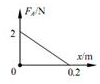
则有,WA=-$\frac{1}{2}×2×0.2×2$=-0.4J
解得:W=-WG-WA=1.5+0.4=1.9J;
答:(1)线圈ab边运动到x=0.1m位置时,线圈受到的安培力1N.
(2)线圈穿过磁场区域过程中拉力F 做的总功1.9J.
点评 考查法拉第电磁感应定律,闭合电路欧姆定律的内容,掌握安培力表达式与动能定理的应用,理解根据FA-x图象求得总功的方法.

练习册系列答案
相关题目
5.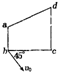 如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd,ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,e为质子的电量,不计质子的重力,则( )
如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd,ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,e为质子的电量,不计质子的重力,则( )
 如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd,ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,e为质子的电量,不计质子的重力,则( )
如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd,ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,e为质子的电量,不计质子的重力,则( )| A. | c点电势为12V | |
| B. | 场强的方向由a指向c | |
| C. | 质子从b运动到c所用的时间为 $\frac{\sqrt{2}l}{{v}_{0}}$ | |
| D. | 质子从b运动到c电场力做功12eV |
6.如果把太阳系各行星的运动近似看作匀速圆周运动,则离太阳越近的行星( )
| A. | 周期越小 | B. | 环绕速度越小 | C. | 角速度越小 | D. | 加速度越小 |
7.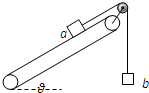 如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中,以下说法错误的是( )
如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中,以下说法错误的是( )
 如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中,以下说法错误的是( )
如图所示,足够长的传送带与水平方向的倾角为θ,物块a通过平行于传送带的轻绳跨过光滑轻滑轮与物块b相连,b的质量为m.开始时,a、b及传送带均静止,且a不受传送带摩擦力作用,现让传送带逆时针匀速转动,则在b上升h高度(未与滑轮相碰)过程中,以下说法错误的是( )| A. | 物块a的重力势能减少mgh | |
| B. | 摩擦力对a做的功等于a机械能的增量 | |
| C. | 摩擦力对a做的功等于物块a、b动能增量之和 | |
| D. | 任意时刻,重力对a、b做功的瞬时功率大小相等 |
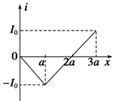
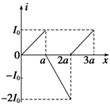
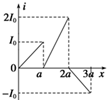
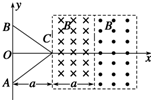 如图所示,两个垂直纸面的匀强磁场方向相反,磁感应强度的大小均为B,磁场区域宽度均为a,一正三角形(中垂线长为a)导线框ABC从图示位置沿x轴正方向匀速穿过两磁场区域,以逆时针方向为电流的正方向,下列选项中感应电流i与线框移动距离x的关系图象正确的是( )
如图所示,两个垂直纸面的匀强磁场方向相反,磁感应强度的大小均为B,磁场区域宽度均为a,一正三角形(中垂线长为a)导线框ABC从图示位置沿x轴正方向匀速穿过两磁场区域,以逆时针方向为电流的正方向,下列选项中感应电流i与线框移动距离x的关系图象正确的是( )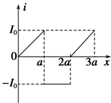

 如图所示,在花园里,水管中射出的水流呈现一道美丽的弧线,如果水喷出管口的速度是10m/s,管口与水平方向的夹角为30°,空气阻力不计,取g=10m/s2,试计算水的射程为多少?
如图所示,在花园里,水管中射出的水流呈现一道美丽的弧线,如果水喷出管口的速度是10m/s,管口与水平方向的夹角为30°,空气阻力不计,取g=10m/s2,试计算水的射程为多少?