题目内容
10.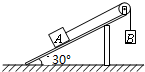 如图所示,用细绳连接的两个物体A、B,跨过一光滑定滑轮放于一倾角为30°的光滑斜面上,两物体距水平面的高度均为斜面高度的一半,静止开始释放两物体后,A恰能到达斜面的顶端,求A、B两物体的质量之比是多少?
如图所示,用细绳连接的两个物体A、B,跨过一光滑定滑轮放于一倾角为30°的光滑斜面上,两物体距水平面的高度均为斜面高度的一半,静止开始释放两物体后,A恰能到达斜面的顶端,求A、B两物体的质量之比是多少?
分析 A、B开始运动到B着地过程中,系统的机械能守恒,运用机械能守恒定律求出它们的速度表达式.B着地后,A继续沿斜面做匀减速运动,当速度减为零时,A能沿斜面滑行的距离最大.对A运用机械能守恒列式,联立可求解.
解答 解:设斜面的高度为2h.设B刚落地时的速度为v,系统的机械能守恒:
mBgh-mAghsin30°=$\frac{1}{2}$(mA+mB)v2
B落地后,A以v为初速度沿斜面匀减速上升,沿斜面又上升的高度为:h-hsin30°=0.5h
对A,由机械能守恒得:-mAg•0.5h=0-$\frac{1}{2}$mAv2
联立解得:$\frac{{m}_{A}}{{m}_{B}}$=$\frac{1}{2}$
答:A、B两物体的质量之比是1:2.
点评 本题是两个过程的问题,两个物体连在一起时,A、B单个物体机械能不守恒,但二者组成的系统机械能守恒.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
20.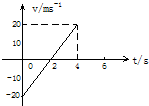 (多选)如图所示,图象为一物体做匀变速直线运动的v-t图象.由图象作出的下列判断,其中正确的是( )
(多选)如图所示,图象为一物体做匀变速直线运动的v-t图象.由图象作出的下列判断,其中正确的是( )
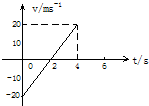 (多选)如图所示,图象为一物体做匀变速直线运动的v-t图象.由图象作出的下列判断,其中正确的是( )
(多选)如图所示,图象为一物体做匀变速直线运动的v-t图象.由图象作出的下列判断,其中正确的是( )| A. | 物体始终沿正方向运动 | |
| B. | 物体先沿负方向运动,在t=2s后沿正方向运动 | |
| C. | 在t=2s时,物体距出发点最远 | |
| D. | 在t=2s前物体位于出发点负方向上,t=2s后位 于出发点正方向上 |
1.第一次通过实验比较准确地测出万有引力常量的科学家是( )
| A. | 丹麦的第谷 | B. | 德国的开普勒 | C. | 英国的牛顿 | D. | 英国的卡文迪许 |
5.质量为m的物体始终固定在倾角为θ的斜面上,下列说法正确的是( )
| A. | 若斜面水平向右匀速运动距离l,斜面对物体没有做功 | |
| B. | 若斜面向上匀速运动距离l,斜面对物体做功为mgl | |
| C. | 若斜面水平向左以加速度a运动距离l,斜面对物体做功为mal | |
| D. | 若斜面向下以加速度a运动距离l,斜面对物体做功为m(g+a)l |
4.质量为m的物体,在距地面h高处以$\frac{1}{3}$g的加速度由静止竖直下落到地面,下列说法中正确的是( )
| A. | 物体重力势能减少$\frac{1}{3}$mgh | B. | 物体的机械能减少$\frac{1}{3}$mgh | ||
| C. | 物体的动能增加mgh | D. | 重力做功mgh |
1.两颗行星的质量分别为m1和m2,它们绕太阳运行的轨道半径分别是r1和r2,若它们只受太阳引力的作用,那么这两颗行星的向心加速度之比为( )
| A. | 1 | B. | $\frac{{m}_{2}{r}_{1}}{{m}_{1}{r}_{2}}$ | C. | $\frac{{m}_{1}{r}_{2}}{{m}_{2}{r}_{1}}$ | D. | $\frac{{{r}_{2}}^{2}}{{{r}_{1}}^{2}}$ |
2.下列实验或器件应用涡流现象的是( )
| A. |  电磁感应实验 | B. |  日光灯电路 | C. |  直流电动机 | D. |  电磁灶 |
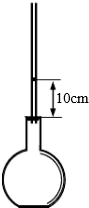 如图所示为某同学设计的一只简易温度计,图中瓶塞表面与烧瓶瓶口齐平,一根粗细均匀、管内横截面积为S=0.6cm2、两端开口的细玻璃管插入瓶塞中,玻璃管内有一小段红色液柱封住一定质量的气体.已知瓶口下方气体的体积为60cm3.
如图所示为某同学设计的一只简易温度计,图中瓶塞表面与烧瓶瓶口齐平,一根粗细均匀、管内横截面积为S=0.6cm2、两端开口的细玻璃管插入瓶塞中,玻璃管内有一小段红色液柱封住一定质量的气体.已知瓶口下方气体的体积为60cm3.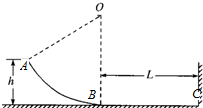 如图所示高度h=0.6m的光滑圆弧形轨道AB在B点与长为L=1.2m的水平粗糙轨道BC相切,在C点固定一竖直挡板,质量m=1kg的小球从A点由静止滑下,小球沿轨道ABC运动并与挡板发生碰撞,已知∠AOB=60°,圆心为O,取g=10m/s2.求:
如图所示高度h=0.6m的光滑圆弧形轨道AB在B点与长为L=1.2m的水平粗糙轨道BC相切,在C点固定一竖直挡板,质量m=1kg的小球从A点由静止滑下,小球沿轨道ABC运动并与挡板发生碰撞,已知∠AOB=60°,圆心为O,取g=10m/s2.求: