题目内容
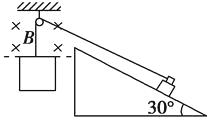
【题目】如图所示，光滑水平面上有一质量为2M、半径为R（R足够大）的圆弧曲面C，质量为M的小球B置于其底端，另一个小球A质量为 
，以v0=6m/s的速度向B运动，并与B发生弹性碰撞，不计一切摩擦，小球均视为质点，求：
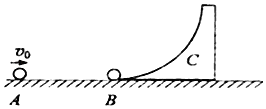
（1）小球B的最大速率；
（2）小球B运动到圆弧曲面最高点时的速率；
（3）通过计算判断小球B能否与小球A再次发生碰撞．
【答案】
（1）
解：A与B发生弹性碰撞，取水平向右为正方向，根据动量守恒定律和动能守恒得：
v0= vA+MvB；
由动能守恒得： 
v02= vA2+ MvB2；
解得 vA=﹣2m/s，vB=4m/s
故B的最大速率为4m/s
（2）
解：B冲上C并运动到最高点时二者共速设为v，则
MvB=（M+2M）v
可以得到：v= 
m/s
（3）
解：从B冲上C然后又滑下的过程，设BC分离时速度分别为vB′、vC′．
由水平动量守恒有
MvB=MvB′+2MvC′
机械能也守恒，有 MvB2= MvB′2+ 2MvC′2
联立可以得到：vB′=﹣ m/s
由于|vB′|＜|vA|，所有二者不会再次发生碰撞
【解析】（1）A与B发生弹性碰撞，碰后B的速率最大，由动量守恒定律和动能守恒结合求小球B的最大速率；（2）小球B运动到圆弧曲面最高点时B与C共速，由水平方向动量守恒求B的速率；（3）根据B、C系统的水平方向动量守恒和机械能守恒求出小球B返回C的底端时的速率，与A的速率比较，分析B能否与小球A再次发生碰撞．
【考点精析】认真审题，首先需要了解功能关系(当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1)，还要掌握动量守恒定律(动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变)的相关知识才是答题的关键．
