题目内容
建筑工地有一种“深坑打夯机”。工作时,电动机带动两个紧压夯杆的滚轮匀速转动可将夯杆从深为h=6.4m的坑中提上来。当夯杆底端升至坑口时,夯杆被释放,最后夯杆在自身重力作用下,落回深坑,夯实坑底。之后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作。已知两个滑轮边缘的线速度v恒为4m/s,每个滚轮对夯杆的正压力F=2×104N,滚轮与夯杆间的动摩擦因素µ=0.3,夯杆质量m=1×103kg,坑深h=6.4m。假定在打夯过程中坑的深度变化不大,.取g=10m/s2,求:
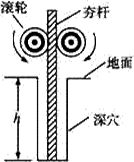
(1)每个打夯周期中 电动机对夯杆所做的功;
(2)每个打夯周期中滑轮对夯杆间因摩擦而产生的热量;
(3)打夯周期

(1)每个打夯周期中 电动机对夯杆所做的功;
(2)每个打夯周期中滑轮对夯杆间因摩擦而产生的热量;
(3)打夯周期
(1)7.2×104J(2)4.8×104J(3)4.2s
本题中主要是分析出各个过程中的受力情况,再根据牛顿第二定律求出加速度,确定运动性质求出相关物理量
(1) 夯杆上升过程中电动机带动滚轮对夯杆做功,加速上升阶段夯杆加速度
a=(2μF-mg)/m=2m/s2?
位移s1=v2/2a=4m,?
滚轮对夯杆做功?
W1=2μFS1=4.8×104J?
匀速上升阶段滚轮对夯杆的摩擦力突变为静摩擦力,夯杆的位移?
S2=h-S1=2.4m?
摩擦力做功?
W2=mgS2=2.4×104J?
所以每个打夯周期电动机对夯杆做功?
W=W1+W2=7.2×104J?
(2)夯杆加速上升阶段滚轮与夯杆间摩擦生热,加速时间?
t=v/a=2s?
两物间相对位移?
S相对=S轮-S杆?
=v t-S1
=4m?
滚轮与夯杆间摩擦生热?
Q=2μFS相对
=4.8×104J?
⑶夯杆离开滚轮后继续上升到最高点经历时间是t3=v/g=0.4s,上升高度h3=0.8m;接着自由下落h4=7.2m,经历时间t4=1.2s。因此打夯周期T=t1+t2+t3+t4=4.2s。
(1) 夯杆上升过程中电动机带动滚轮对夯杆做功,加速上升阶段夯杆加速度
a=(2μF-mg)/m=2m/s2?
位移s1=v2/2a=4m,?
滚轮对夯杆做功?
W1=2μFS1=4.8×104J?
匀速上升阶段滚轮对夯杆的摩擦力突变为静摩擦力,夯杆的位移?
S2=h-S1=2.4m?
摩擦力做功?
W2=mgS2=2.4×104J?
所以每个打夯周期电动机对夯杆做功?
W=W1+W2=7.2×104J?
(2)夯杆加速上升阶段滚轮与夯杆间摩擦生热,加速时间?
t=v/a=2s?
两物间相对位移?
S相对=S轮-S杆?
=v t-S1
=4m?
滚轮与夯杆间摩擦生热?
Q=2μFS相对
=4.8×104J?
⑶夯杆离开滚轮后继续上升到最高点经历时间是t3=v/g=0.4s,上升高度h3=0.8m;接着自由下落h4=7.2m,经历时间t4=1.2s。因此打夯周期T=t1+t2+t3+t4=4.2s。

练习册系列答案
相关题目
 =0.3,g取1Om/s2,求:
=0.3,g取1Om/s2,求: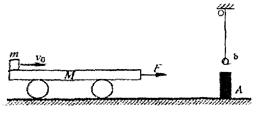

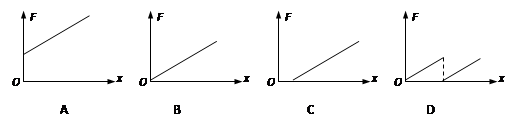
 ,物体向上运动的加速度为a,在物体上升h的过程中,力F做的功为( )
,物体向上运动的加速度为a,在物体上升h的过程中,力F做的功为( )
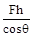
 的光滑绝缘斜面上放置质量分别为m、2m相距L可视为点电荷的带电小球A、B将小球A、B同时无初速释放,已知释放瞬时小球A的加速度为零,经过一段时间,小球A、B间的距离为x时,两者的加速度大小分别为aA、aB大小关系为aB -1.5aA,重力加速度为g,则以下说法
的光滑绝缘斜面上放置质量分别为m、2m相距L可视为点电荷的带电小球A、B将小球A、B同时无初速释放,已知释放瞬时小球A的加速度为零,经过一段时间,小球A、B间的距离为x时,两者的加速度大小分别为aA、aB大小关系为aB -1.5aA,重力加速度为g,则以下说法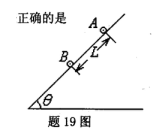
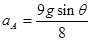
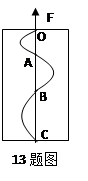
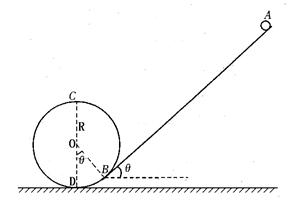
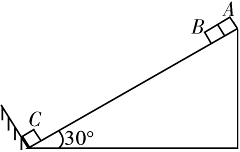
 的斜面和半径为R的光滑圆环组成。假设小球从A处由静止释放,沿着动摩擦因数为
的斜面和半径为R的光滑圆环组成。假设小球从A处由静止释放,沿着动摩擦因数为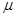 的斜面运动到B点(B为斜面与圆环的切点),而后沿光滑圆环内侧运动,若小球刚好能通过圆环的最高点C。 (重力加速度为g)
的斜面运动到B点(B为斜面与圆环的切点),而后沿光滑圆环内侧运动,若小球刚好能通过圆环的最高点C。 (重力加速度为g)