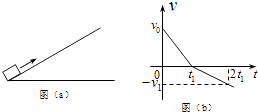题目内容
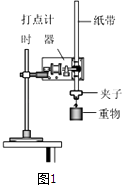
【题目】某实验小组利用图1所示的装置探究加速度与力、质量的关系.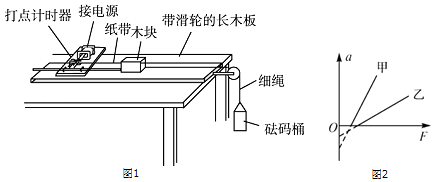
(1)下列做法正确的是 (填字母代号).
A.调节滑轮的高度,使牵引木块的细绳与长木板保持平行
B.在调节木板倾斜度平衡木块受到的滑动摩擦力时,将装有砝码的砝码桶通过定滑轮拴在木块上
C.实验时,先放开木块再接通打点计时器的电源
D.通过增减木块上的砝码改变质量时,不需要重新调节木板倾斜度
(2)为使砝码桶及桶内砝码的总重力在数值上近似等于木块运动时受到的拉力,应满足的条件是砝码桶及桶内砝码的总质量木块和木块上砝码的总质量.(填“远大于”“远小于”或“近似等于”)
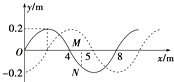
(3)甲、乙两同学在同一实验室,各取一套装置放在水平桌面上,木块上均不放砝码,在没有平衡摩擦力的情况下,研究加速度a与拉力F的关系,分别得到图2中甲、乙两条直线.设甲、乙用的木块质量分别为m甲、m乙 , 甲、乙用的木块与木板间的动摩擦因数分别为μ甲、μ乙 , 由图2可知,μ甲μ乙 , m甲m乙 . (填“大于”“小于”或“等于”)
【答案】
(1)A,D
(2)远小于
(3)小于,大于
【解析】解:(1)A、调节滑轮的高度,使牵引木块的细绳与长木板保持平行,否则拉力不会等于合力,A符合题意;
B、在调节模板倾斜度平衡木块受到的滑动摩擦力时,不应悬挂“重物”,B不符合题意;
C、打点计时器要“早来晚走”即实验开始时先接通打点计时器的电源待其平稳工作后再释放木块,而当实验结束时应先控制木块停下再停止打点计时器,C不符合题意;
D、平衡摩擦力后,有mgsinθ=μmgcosθ,即μ=tanθ,与质量无关,故通过增减木块上的砝码改变质量时,不需要重新调节木板倾斜度,D符合题意;选择AD;(2)设砝码与砝码桶的质量为m,小车的质量为M,对砝码桶及砝码与小车组成的系统,由牛顿第二定律得:a= ![]() ,
,
对木块,由牛顿第二定律得:T=Ma= ![]() =
= ![]() ,
,
只有当 a= ![]() <
< ![]() ,只有当砝码桶及桶的质量远小于小车质量时,即:m<<M时,小车受到的拉力近似等于砝码及砝码桶的重力;(3)当没有平衡摩擦力时有:T﹣f=ma,故a=
,只有当砝码桶及桶的质量远小于小车质量时,即:m<<M时,小车受到的拉力近似等于砝码及砝码桶的重力;(3)当没有平衡摩擦力时有:T﹣f=ma,故a= ![]() T﹣μg,即图线斜率为
T﹣μg,即图线斜率为 ![]() ,纵轴截距的大小为μg.观察图线可知m甲小于m乙,μ甲大于μ乙;
,纵轴截距的大小为μg.观察图线可知m甲小于m乙,μ甲大于μ乙;
答案为:(1)AD;(2)远小于;(3)小于,大于.
理解平衡摩擦力的深刻含义,能够运用数学上函数图像相关知识分析本题即可求解。本实验同时要注意平衡摩擦力时不要挂重物,整个实验平衡了摩擦力后,不管以后是改变砝码和盘的质量还是改变小车及砝码的质量,都不需要重新平衡摩擦力。

【题目】某物理课外小组利用图(a)中的装置探究物体加速度与其所受合外力之间的关系.图中,置于实验台上的长木板水平放置,其右端固定一轻滑轮;轻绳跨过滑轮,一端与放在木板上的小滑车相连,另一端可悬挂钩码.本实验中可用的钩码共有N=5个,每个质量均为0.010kg.实验步骤如下: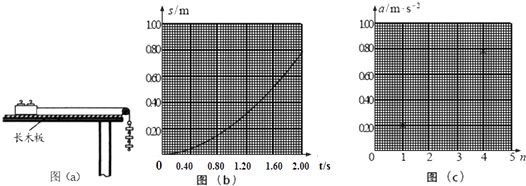
①将5个钩码全部放入小车中,在长木板左下方垫上适当厚度的小物快,使小车(和钩码)可以在木板上匀速下滑.
②将n(依次取n=1,2,3,4,5)个钩码挂在轻绳右端,其余N﹣n个钩码仍留在小车内;用手按住小车并使轻绳与木板平行.释放小车,同时用传感器记录小车在时刻t相对于其起始位置的位移s,绘制s﹣t图象,经数据处理后可得到相应的加速度a.
(1)对应于不同的n的a值见下表.n=2时的s﹣t图象如图(b)所示;由图(b)求出此时小车的加速度(保留2位有效数字),将结果填入下表.
n | 1 | 2 | 3 | 4 | 5 |
a/ms﹣2 | 0.20 | 0.58 | 0.78 | 1.00 |
(2)利用表中的数据在图(c)中补齐数据点,并作出a﹣n图象.从图象可以看出:当物体质量一定时,物体的加速度与其所受的合外力成正比.
(3)利用a﹣n图象求得小车(空载)的质量为 kg(保留2位有效数字,重力加速度取g=9.8ms﹣2).
(4)若以“保持木板水平”来代替步骤①,下列说法正确的是 (填入正确选项前的标号)
A.a﹣n图线不再是直线
B.a﹣n图线仍是直线,但该直线不过原点
C.a﹣n图线仍是直线,但该直线的斜率变大.