题目内容
由于两个物体相对位置的变化会引起引力场的能量变化,这种能量被称作这一对物体的引力势能.如果以无限远处的势能为0,则万有引力势能EP可用下式进行计算: ,式中m、M分别代表两个物体的质量,r为相对的物体m到M的中心距离,G为万有引力恒量.假设有两个相同质量均为m=200kg的人造卫星,沿距离地面为地球半径的圆形轨道相向运行,因而经过一段时间后发生了碰撞,碰后两卫星粘合在一起成为一个复合体.不计卫星间的万有引力及空气阻力,(地球半径为R=6400km,地球表面重力加速度取g=10m/s2).求:
,式中m、M分别代表两个物体的质量,r为相对的物体m到M的中心距离,G为万有引力恒量.假设有两个相同质量均为m=200kg的人造卫星,沿距离地面为地球半径的圆形轨道相向运行,因而经过一段时间后发生了碰撞,碰后两卫星粘合在一起成为一个复合体.不计卫星间的万有引力及空气阻力,(地球半径为R=6400km,地球表面重力加速度取g=10m/s2).求:(1)卫星在碰撞之前做圆运动时的速度V的大小;
(2)两卫星碰撞前,系统具有的机械能E;
(3)碰撞后两卫星的复合体落到地面的瞬间的速度v'的大小和方向.
【答案】分析:研究卫星绕地球做圆周运动,其万有引力提供向心力列出等式.
忽略地球自转的影响,根据万有引力等于重力列出等式.
系统具有的机械能等于动能和势能之和.
根据动量守恒得碰撞后复合体得速度为0,再根据机械能守恒求解落到地面的瞬间的速度.
解答:解:(1)设卫星做圆周运动的速度为v,其万有引力提供向心力得:
 =m
=m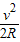
在地球表面: =mg
=mg
解得:v=5.66km/s
(2)碰撞前两卫星与地球组成的系统总机械能为:
E=2( mv2-
mv2-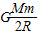 )
)
联立以上各式,代入数值解得:
E=- mgR=-6.4×109 J
mgR=-6.4×109 J
(3)设碰撞后组成的复合体速度为v1,
根据动量守恒得:mv-mv=2mv1
解得:v1=0
此时复合体由静止开始自由下落,由机械能守恒得:
- =
= ?2m?v′2-
?2m?v′2-
解得:v′=8km/s
速度方向竖直向下.
答:(1)卫星在碰撞之前做圆运动时的速度V的大小是5.66km/s;
(2)两卫星碰撞前,系统具有的机械能是-6.4×109 J;
(3)碰撞后两卫星的复合体落到地面的瞬间的速度的大小是8km/s和方向竖直向下.
点评:本题考查了多个知识点的应用,要能根据求解的问题选择恰当的物理规律求解.
运用黄金代换式GM=gR2求出问题是考试中常见的方法.
忽略地球自转的影响,根据万有引力等于重力列出等式.
系统具有的机械能等于动能和势能之和.
根据动量守恒得碰撞后复合体得速度为0,再根据机械能守恒求解落到地面的瞬间的速度.
解答:解:(1)设卫星做圆周运动的速度为v,其万有引力提供向心力得:
 =m
=m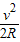
在地球表面:
 =mg
=mg解得:v=5.66km/s
(2)碰撞前两卫星与地球组成的系统总机械能为:
E=2(
 mv2-
mv2-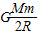 )
)联立以上各式,代入数值解得:
E=-
 mgR=-6.4×109 J
mgR=-6.4×109 J(3)设碰撞后组成的复合体速度为v1,
根据动量守恒得:mv-mv=2mv1
解得:v1=0
此时复合体由静止开始自由下落,由机械能守恒得:
-
 =
= ?2m?v′2-
?2m?v′2-
解得:v′=8km/s
速度方向竖直向下.
答:(1)卫星在碰撞之前做圆运动时的速度V的大小是5.66km/s;
(2)两卫星碰撞前,系统具有的机械能是-6.4×109 J;
(3)碰撞后两卫星的复合体落到地面的瞬间的速度的大小是8km/s和方向竖直向下.
点评:本题考查了多个知识点的应用,要能根据求解的问题选择恰当的物理规律求解.
运用黄金代换式GM=gR2求出问题是考试中常见的方法.

练习册系列答案
相关题目
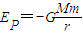 ,式中m、M分别代表两个物体的质量,r为相对的物体m到M的中心距离,G为万有引力恒量.假设有两个相同质量均为m=200kg的人造卫星,沿距离地面为地球半径的圆形轨道相向运行,因而经过一段时间后发生了碰撞,碰后两卫星粘合在一起成为一个复合体.不计卫星间的万有引力及空气阻力,(地球半径为R=6400km,地球表面重力加速度取g=10m/s2).求:
,式中m、M分别代表两个物体的质量,r为相对的物体m到M的中心距离,G为万有引力恒量.假设有两个相同质量均为m=200kg的人造卫星,沿距离地面为地球半径的圆形轨道相向运行,因而经过一段时间后发生了碰撞,碰后两卫星粘合在一起成为一个复合体.不计卫星间的万有引力及空气阻力,(地球半径为R=6400km,地球表面重力加速度取g=10m/s2).求:


 =
= 
















