题目内容
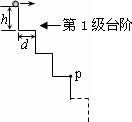
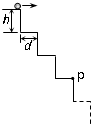 如图所示,小球从台阶顶部以一定的水平速度向右抛出,已知每级台阶的高为h=60cm,宽为d=40cm,台阶级数足够多,忽略一切阻力,取g=10m/s2,
如图所示,小球从台阶顶部以一定的水平速度向右抛出,已知每级台阶的高为h=60cm,宽为d=40cm,台阶级数足够多,忽略一切阻力,取g=10m/s2,(1)若要使小球击中P点(第3级台阶末端),求小球的初速度大小;
(2)若小球的初速度大小为5.0m/s,求小球从抛出至第一次击中台阶的过程中下落的高度.
分析:(1)根据高度求出平抛运动的时间,结合水平位移和时间求出小球的初速度大小.
(2)连接每级台阶的末端成一斜面,当小球落到斜面时,结合平抛运动的规律,抓住竖直位移与水平位移的关系求出水平位移,确定落在第几级台阶上,从而得出下落的高度.
(2)连接每级台阶的末端成一斜面,当小球落到斜面时,结合平抛运动的规律,抓住竖直位移与水平位移的关系求出水平位移,确定落在第几级台阶上,从而得出下落的高度.
解答:解:(1)小球的水平位移 v0t1=3d
小球的竖直位移
g
=3h
联立,代入数据得 v0=2.0m/s
(2)连接每级台阶的末端成一斜面,当小球落到斜面时,
x=vt2
y=
g
=
联立,代入数据得:x=7.5m
令n=
=
=18.75,说明小球击中第19级台阶
即小球从抛出至第一次击中台阶下落的高度为:H=19h=19×0.6m=11.4m
答:(1)小球的初速度大小为2m/s.
(2)小球从抛出至第一次击中台阶的过程中下落的高度为11.4m.
小球的竖直位移
| 1 |
| 2 |
| t | 2 1 |
联立,代入数据得 v0=2.0m/s
(2)连接每级台阶的末端成一斜面,当小球落到斜面时,
x=vt2
y=
| 1 |
| 2 |
| t | 2 2 |
| y |
| x |
| h |
| d |
联立,代入数据得:x=7.5m
令n=
| x |
| d |
| 7.5 |
| 0.4 |
即小球从抛出至第一次击中台阶下落的高度为:H=19h=19×0.6m=11.4m
答:(1)小球的初速度大小为2m/s.
(2)小球从抛出至第一次击中台阶的过程中下落的高度为11.4m.
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
如图所示,小球从楼梯上以2m/s的速度水平抛出,所有台阶的高度和宽度均为0.25m,g取10m/s2,小球抛出后首先落到的台阶是( )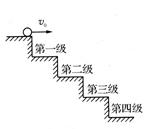
| A.第一级台阶 | B.第二级台阶 |
| C.第三级台阶 | D.第四级台阶 |
 (2013?湖南模拟)如图所示,小球从楼梯上以2m/s的速度水平抛出,所有台阶的高度和宽度均为0.25m,g取10/s2,小球抛出后首先落到的台阶是( )
(2013?湖南模拟)如图所示,小球从楼梯上以2m/s的速度水平抛出,所有台阶的高度和宽度均为0.25m,g取10/s2,小球抛出后首先落到的台阶是( ) 如图所示,小球从台阶顶部以一定的水平速度向右抛出,已知每级台阶的高为h=60cm,宽为d=40cm,台阶级数足够多,忽略一切阻力,取g=10m/s2,
如图所示,小球从台阶顶部以一定的水平速度向右抛出,已知每级台阶的高为h=60cm,宽为d=40cm,台阶级数足够多,忽略一切阻力,取g=10m/s2,