题目内容
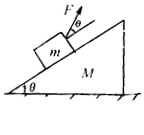
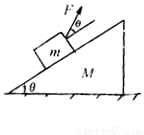
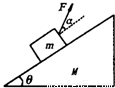
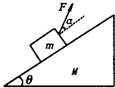 质量为M的木楔倾角为θ,在水平面上保持静止,当将一质量为m的木块放在斜面上时正好匀速下滑,如果用沿与斜面成α角的力F拉着木块匀速上升如图所示.求:
质量为M的木楔倾角为θ,在水平面上保持静止,当将一质量为m的木块放在斜面上时正好匀速下滑,如果用沿与斜面成α角的力F拉着木块匀速上升如图所示.求:(1)当α=?时,拉力F有最小值,求此最小值;
(2)当拉力最小时,水平面对本楔M的摩擦力是多大?
分析:(1)对物块进行受力分析,根据共点力平衡,利用正交分解,在沿斜面方向和垂直于斜面方向都平衡,进行求解
(2)采用整体法,对m、M构成的整体列平衡方程
(2)采用整体法,对m、M构成的整体列平衡方程
解答:解:(1)选木块为研究对象,当没加外力F时正好匀速下滑,设木块与斜面间的滑动摩擦因数为μ,此时平行于斜面方向必有:
mgsinθ=μmgcosθ①
当加上外力F时,对木块受力分析如下图:
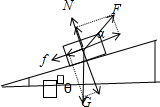
则有:f=μN②
平行于斜面方向:f+mgsinθ=Fcosα③
垂直于斜面方向:N+Fsinα=mgcosθ④
由①②③④解得,F=
⑤
联立①⑤得:F=
故当α=θ时,分母最大,F有最小值,最小值为:
Fmin=mgsin2θ ⑥
(2)选物体和M和m整体为研究对象,设水平面对本楔M的摩擦力是f′,水平方向受力平衡,则有:
f′=Fmincos(θ+α)=Fmincos2θ ⑦
由⑥⑦得,f′=
mgsin4θ
答:(1)当α=θ时,拉力F有最小值为mgsin2θ
(2)当拉力最小时,水平面对本楔M的摩擦力是
mgsin4θ
mgsinθ=μmgcosθ①
当加上外力F时,对木块受力分析如下图:

则有:f=μN②
平行于斜面方向:f+mgsinθ=Fcosα③
垂直于斜面方向:N+Fsinα=mgcosθ④
由①②③④解得,F=
| 2mgsinθ |
| cosα+μsinα |
联立①⑤得:F=
| mgsin2θ | ||
sin(
|
故当α=θ时,分母最大,F有最小值,最小值为:
Fmin=mgsin2θ ⑥
(2)选物体和M和m整体为研究对象,设水平面对本楔M的摩擦力是f′,水平方向受力平衡,则有:
f′=Fmincos(θ+α)=Fmincos2θ ⑦
由⑥⑦得,f′=
| 1 |
| 2 |
答:(1)当α=θ时,拉力F有最小值为mgsin2θ
(2)当拉力最小时,水平面对本楔M的摩擦力是
| 1 |
| 2 |
点评:木块放在斜面上时正好匀速下滑隐含摩擦系数的数值恰好等于斜面倾角的正切值,当有外力作用在物体上时,列平行于斜面方向的平衡方程,找到外力F的表达式,讨论F取最小值的条件,求解第二问时,灵活选用整体的思想较好,总体上看此题有一定难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
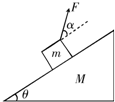 质量为M的木楔倾角为θ,在水平面上保持静止,当将一质量为m的木块放在斜面上时正好匀速下滑.如果用与斜面成α角的力F拉着木块匀速上升,如图所示,求:
质量为M的木楔倾角为θ,在水平面上保持静止,当将一质量为m的木块放在斜面上时正好匀速下滑.如果用与斜面成α角的力F拉着木块匀速上升,如图所示,求: