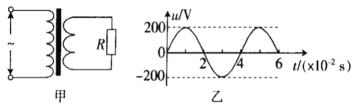
题目内容
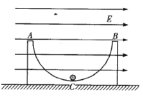
【题目】如图所示,AB为一光滑固定轨道,AC为动摩擦因数μ=0.25的粗糙水平轨道,O为水平地面上的一点,且B、C、O在同一竖直线上,已知B、C两点的高度差为h,C、O两点的高度差也为h,AC两点相距s=2h. 若质量均为m的两滑块P、Q从A点以相同的初速度v0分别沿两轨道滑行,到达B点或C点后分别水平抛出.求:
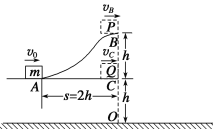
(1)两滑块P、Q落地点到O点的水平距离.
(2)欲使两滑块的落地点相同,滑块的初速度v0应满足的条件.
(3)若滑块Q的初速度v0已满足(2)的条件,现将水平轨道AC向右延伸一段L,要使滑块Q落地点距O点的距离最远,L应为多少?
【答案】(1)![]() ,
, ![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)利用动能定理分别求出到达BC点的速度,利用平抛运动求的水平位移;(2)利用两位移相等即可求得速度;(3)利用动能定理求出平抛运动的速度,有数学关系求的即可.
(1)滑块P从A到B的过程中由动能定理可知:![]()
可得:![]()
从B点抛出x1=vBtP
![]()
解得:![]()
滑块Q从A到C过程,由动能定理得:![]()
解得:![]()
从C点抛出:![]() ,
,![]()
解得:![]()
(2)要使x1=x2,联立解得:![]()
(3)由动能定理得: ![]()
在延伸最右端抛出: ![]() ,
,![]()
距O点的距离为△x=L+x
得:![]() ,当
,当![]() 时,△x取最大值
时,△x取最大值![]()

练习册系列答案
相关题目