题目内容
【题目】如图所示，水平转台的半径为0.2m，在离转轴0.12m处，立一根直杆，杆顶系一根长0.3m的细线，线的另一端拴一个0.1kg的小球，当转台匀速转动时，小球随着转台一起作匀速圆周运动，拴小球的细线与直杆之间成37°角（sin37°=0.6，cos37°=0.8）．
求：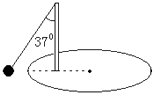
（1）细线的拉力？
（2）转台的角速度？
【答案】
（1）
解：根据小球竖直方向受力平衡，则有：
mg=Tcos37°
解得：T= 
=1.25N
（2）
解：根据圆周运动向心力公式得：
Tsin37°=mω2r=mω2（0.12+0.3sin37°）
解得：ω=5rad/s
【解析】（1）根据小球竖直方向受力平衡，结合几何关系即可求解；（2）根据向心力公式即可求解．
【考点精析】根据题目的已知条件，利用向心力的相关知识可以得到问题的答案，需要掌握向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
