��Ŀ����
14����ͼ��ʾ����Ǧ�=30����㹻��ƽ�е���MN��M��N����ˮƽ���õ�ƽ�е���NP��N��P��ƽ�����ӣ��������ΪL��MM��������ֵΪR�ĵ��裬����⻬�ҵ��費�ƣ���б����MN��M��N��֮�䣨������з���ֱ����ƽ�����ϵ���ǿ�ų���ˮƽ���ֵ�ee��ff��֮�䣨���������ֱ���ϡ��Ÿ�Ӧǿ��ΪB2����ǿ�ų����ų�����Ϊd������Ϊm������Ϊr�������Դ���L�ĵ����ab�ӿ�������϶˵�ijλ���ɾ�ֹ��ʼ�»�����ʼ���뵼�촹ֱ���Ӵ����ã�����ee���ff��λ��ʱ�����ʷֱ�Ϊv��$\frac{v}{4}$����֪�����ab����������˶�ʱ�����ٶȵļ�С�������ڴų���ͨ���ľ�������ȣ�����v�ء�x��
��1�����������ǿ�ų��ĴŸ�Ӧǿ��B1��
��2�������abͨ�����������е���R�����Ľ����ȣ�
��3���ı�B1ʹ�����ab���ܴ���������赼���ab�Ӿ���ee�䵽ֹͣͨ������R�ĵ���Ϊq����B1��ȡֵ��Χ����q��B1�Ĺ�ϵʽ��
���� ��1�����ڵ����㹻������ab�����ﵼ���NN��ǰ�Ѿ��������˶�������ƽ�������Ͱ�������ʽ���B1��
��2����ab���͵���R�����ĵ��ȷֱ�ΪQr��QR������$\frac{{Q}_{R}}{{Q}_{r}}$=$\frac{R}{r}$�����������غ��غ㶨����⣮
��3��������ٶ�vxͨ��ee��ʱ����������л���x��ͣ�£����⣬��v�ء�x���ɵ� vx=$\frac{v-\frac{v}{4}}{a}$x=$\frac{3x}{4d}$v�����ݰ������˶�ʱ����ƽ�⣬��ʽ�õ�B1��x�Ĺ�ϵʽ��ʹ�����ab���ܴ��������Ӧ����x��d���õ���ӦB1��ȡֵ��Χ���ٸ��ݷ����ڵ�Ÿ�Ӧ���ɺ�ŷķ������������
��� �⣺��1���ɵ����㹻����֪ab���ﵼ���NN��ǰ�Ѿ��������˶�������Ϊv�����ʱab�����ĵ綯��ΪE������ΪI������
E=B1Lv ��
I=$\frac{E}{R+r}$ ��
��ƽ�������� mgsin��=B1IL ��
�����٢ڢ۽�� B1=$\frac{1}{L}$$\sqrt{\frac{mg��R+r��}{2v}}$ ��
��2����ab���͵���R�����ĵ��ȷֱ�ΪQr��QR������
$\frac{{Q}_{R}}{{Q}_{r}}$=$\frac{R}{r}$ ��
�������غ��غ㶨�ɵ� $\frac{1}{2}m{v}^{2}$=$\frac{1}{2}m��\frac{v}{4}��^{2}$+QR+Qr ��
�����ݢ�� QR=$\frac{15m{v}^{2}R}{32��R+r��}$ ��
��3��������ٶ�vxͨ��ee��ʱ����������л���x��ͣ�£���������
vx=$\frac{v-\frac{v}{4}}{a}$x=$\frac{3x}{4d}$v ��
��������˶�ʱ�����ĵ綯��ΪEx������ΪIx������
mgsin��=B1IxL ��
Ex=B1Lvx ��
Ix=$\frac{{E}_{x}}{R+r}$
������� B1=$\frac{1}{L}$$\sqrt{\frac{2mgd��R+r��}{3vx}}$��
ʹ�����ab���ܴ��������Ӧ����x��d����ӦB1��ȡֵ��Χ��
B1��$\frac{1}{L}$$\sqrt{\frac{2mg��R+r��}{3v}}$
��ab��ͨ��ee'������x��ͣ�£�ʱ��Ϊ��t����˹���
��������ƽ���綯�� $\overline{E}$=$\frac{����}{��t}$=$\frac{{B}_{2}Lx}{��t}$
��·��ƽ������ $\overline{I}$=$\frac{\overline{E}}{R+r}$
ͨ������R�ĵ��� q=$\overline{I}$��t
������� q=$\frac{2{B}_{2}mgd}{3{B}_{1}^{2}Lv}$ ��B1��$\frac{1}{L}$$\sqrt{\frac{2mg��R+r��}{3v}}$����
�𣺣�1���������ǿ�ų��ĴŸ�Ӧǿ��B1��$\frac{1}{L}$$\sqrt{\frac{mg��R+r��}{2v}}$��
��2�������abͨ�����������е���R�����Ľ�������$\frac{15m{v}^{2}R}{32��R+r��}$��
��3��B1��ȡֵ��ΧΪB1��$\frac{1}{L}$$\sqrt{\frac{2mg��R+r��}{3v}}$��q��B1�Ĺ�ϵʽΪq=$\frac{2{B}_{2}mgd}{3{B}_{1}^{2}Lv}$ ��B1��$\frac{1}{L}$$\sqrt{\frac{2mg��R+r��}{3v}}$����
���� ��������Ϣ�⣬һ������ݵ���������˶�������ƽ����ʽ��������һ���棬ץס������Ϣ�����ٶ���λ�ƵĹ�ϵ�����DZ���Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�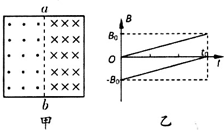 �ڱ߳�ΪL������ΪR�������ε��߿��ڣ��ԶԳ���abΪ�磬��������ֱ�����ŷ�����ͼ����ʾ����ǿ�ų����Դ�ֱֽ������Ĵų�Ϊ���������ִų��ĸ�Ӧǿ��B��ʱ��t�ı仯���ɷֱ���ͼ����ʾ������0-t0ʱ���ڣ����߿��У�������
�ڱ߳�ΪL������ΪR�������ε��߿��ڣ��ԶԳ���abΪ�磬��������ֱ�����ŷ�����ͼ����ʾ����ǿ�ų����Դ�ֱֽ������Ĵų�Ϊ���������ִų��ĸ�Ӧǿ��B��ʱ��t�ı仯���ɷֱ���ͼ����ʾ������0-t0ʱ���ڣ����߿��У�������| A�� | ��Ӧ���� | |
| B�� | ��Ӧ������� | |
| C�� | ��Ӧ����Ϊ˳ʱ�뷽��СΪ$\frac{{{L^2}{B_0}}}{{{t_0}R}}$ | |
| D�� | ��Ӧ����Ϊ��ʱ�뷽��СΪ$\frac{{2{L^2}{B_0}}}{{{t_0}R}}$ |
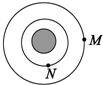
| A�� | M�����������������ȵ�ʱ����ת���ĽǶȽϴ� | |
| B�� | M�Ļ�е�ܴ���N�Ļ�е�� | |
| C�� | M��N���ٶȾ����ڵ�һ�����ٶ� | |
| D�� | M����ͬ��ʱ���ھ�����·�̽϶� |
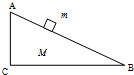 ��ͼ��ʾ��б����ABC����ˮƽ�����ϣ������Ϊ37�㣬������ΪM=5kg���ֽ�һ����Ϊm=3kg��С������б���ϣ���������һ���ij��ٶ�������б�����ϻ������»�������֪б����ABC��û�з����˶����������ٶ�Ϊ10m/s2��sin37��=0.6�������б����ABC�ܵ������֧����N��Ħ����f�Ĵ�С����������Ľ�����ܵ��У�������
��ͼ��ʾ��б����ABC����ˮƽ�����ϣ������Ϊ37�㣬������ΪM=5kg���ֽ�һ����Ϊm=3kg��С������б���ϣ���������һ���ij��ٶ�������б�����ϻ������»�������֪б����ABC��û�з����˶����������ٶ�Ϊ10m/s2��sin37��=0.6�������б����ABC�ܵ������֧����N��Ħ����f�Ĵ�С����������Ľ�����ܵ��У�������| A�� | N=50N��f=40N | B�� | N=87.2N��f=9.6N | C�� | N=72.8N��f=0N | D�� | N=77N��f=4N |
| A�� | ��г�˶�������������� | |
| B�� | �ڵ�����������г�˶��Ļظ�������ʽF=-kx�У�FΪ�������ܵ��ĺ�������kΪ���ɵľ���ϵ�� | |
| C�� | �ڲ����������ϣ�ij���ʵ�����ٶȾ��Dz��Ĵ����ٶ� | |
| D�� | ��˫�����ʵ���У�ͬ�����������Ϲ���ʵ��Ⱥ����ʵ��õ������Ƹ��� |
| A�� | �����϶��µ������� | |
| B�� | �����¶��ϵ������� | |
| C�� | ���������������������϶��£������¶��� | |
| D�� | ���������������������¶��ϣ������϶��� |
| A�� | �ֻ�����ͽ����źŶ������������͵� | |
| B�� | �ֻ�������WiFi�����������ù��ߴ�����Ϣ�� | |
| C�� | ���õ�ң����ͨ�����������������ź���ң�ص��ӻ� | |
| D�� | ���������ߡ������ߡ��������ߵ�Ƶ�����μ�С |
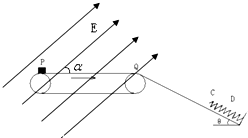 ��ͼ��ʾ��ˮƽ���ʹ�PQ�����L1=1.2m�����ʹ���v0=2m/s���ٶ�˳ʱ�������˶������ʹ�������ˮƽ����ɦ�=37��б���ϵ���ǿ�糡�У��糡ǿ��E=1��103V/m����Ǧ�=30��б��˹̶�һ�ᵯ�ɣ��ᵯ�ɴ���ԭ��ʱ�϶�λ��C�㣬Q����б��ƽ�����ӣ�Q��C��ľ���L2=1.4m����������m=1kg������q=1��10-2C�����壨����Ϊ�ʵ㣩���ٵ�����ڴ��ʹ���˵�P�㣬���屻���͵��Ҷ�Q�����б�����»�����������ѹ�������λ��D���ǡ�ܵ���C�㣮�������徭��Q��ʱ��е�ܵ���ʧ����������������ĵ������ֲ��䣬��֪�����봫�ʹ���б���Ķ�Ħ�������ֱ�Ϊ��1=0.5����2=$\frac{\sqrt{3}}{2}$����gȡ10m/s2��sin37��=0.6��cos37��=0.8������
��ͼ��ʾ��ˮƽ���ʹ�PQ�����L1=1.2m�����ʹ���v0=2m/s���ٶ�˳ʱ�������˶������ʹ�������ˮƽ����ɦ�=37��б���ϵ���ǿ�糡�У��糡ǿ��E=1��103V/m����Ǧ�=30��б��˹̶�һ�ᵯ�ɣ��ᵯ�ɴ���ԭ��ʱ�϶�λ��C�㣬Q����б��ƽ�����ӣ�Q��C��ľ���L2=1.4m����������m=1kg������q=1��10-2C�����壨����Ϊ�ʵ㣩���ٵ�����ڴ��ʹ���˵�P�㣬���屻���͵��Ҷ�Q�����б�����»�����������ѹ�������λ��D���ǡ�ܵ���C�㣮�������徭��Q��ʱ��е�ܵ���ʧ����������������ĵ������ֲ��䣬��֪�����봫�ʹ���б���Ķ�Ħ�������ֱ�Ϊ��1=0.5����2=$\frac{\sqrt{3}}{2}$����gȡ10m/s2��sin37��=0.6��cos37��=0.8������