题目内容
1.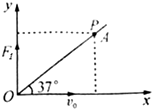 在光滑的水平面内,一质量m=1kg的质点以速度v0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F1=5N作用,质点的运动轨迹与直线OA相交于P点,直线OA与x轴正方向成37°角,如图所示,求:
在光滑的水平面内,一质量m=1kg的质点以速度v0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F1=5N作用,质点的运动轨迹与直线OA相交于P点,直线OA与x轴正方向成37°角,如图所示,求:(1)质点从O点运动到P点所经历的时间;
(2)P点的坐标;
(3)质点到达P点后,撤去恒力F1,改施另一恒力F2,F2作用5s后,质点速度变为零.求恒力F2的大小与方向.
分析 (1)、(2)质点做类平抛运动,将质点的运动分解为x轴方向和y轴方向,在x方向做匀速直线运动,在y方向做匀加速直线运动,结合牛顿第二定律和运动学公式进行分析求解时间和P点的坐标.
(3)由速度时间公式和速度的合成,求出到达P点时的速度,再求出F2作用后的加速度,由牛顿第二定律求F2.
解答 解:(1)质点做类平抛运动,初速度为 v0=10m/s.
设质点在y方向的加速度为a1,则 ${a_1}=\frac{F_1}{m}=5m/{s^2}$
质点到达P点时,有 tan37°=$\frac{y}{x}$=$\frac{\frac{1}{2}{a}_{1}{t}^{2}}{{v}_{0}t}$=$\frac{{a}_{1}t}{2{v}_{0}}$=$\frac{3}{4}$
解得 t=3s
(2)P点的横坐标 x=v0t=10×3=30m
纵坐标 $y=\frac{1}{2}{a_1}{t^2}=\frac{1}{2}×5×9=22.5m$
故P点坐标为(30m,22.5m).
(3)质点到达P点时,vx=v0=10m/s.vy=a1t1=5×3=15m/s
P点的速度大小 $v=\sqrt{v_x^2+v_y^2}=\sqrt{10_{\;}^2+15_{\;}^2}=5\sqrt{13}m/s$,$tanθ=\frac{v_y}{v_x}=\frac{15}{10}=\frac{3}{2}$
即P点的速度方向与x轴正方向的夹角为 θ=arctan$\frac{3}{2}$
撤去恒力F1,改施恒力F2后,质点做匀减速直线运动至速度为零,设质点匀减速运动的加速度大小为a2.
则 a2=$\frac{v}{t′}$=$\frac{5\sqrt{13}}{5}$=$\sqrt{13}$m/s2;
故 F2=ma2=1×$\sqrt{13}$=$\sqrt{13}$N,其方向与速度方向相反,即F2的方向与x轴负方向的夹角为 θ=arctan$\frac{3}{2}$.
答:
(1)质点从O点运动到P点所经历的时间是3s;
(2)P点的坐标为(30m,22.5m);
(3)F2的大小为$\sqrt{13}$N,F2的方向与x轴负方向的夹角为arctan$\frac{3}{2}$.
点评 解决本题的关键对曲线运动的分解,理清分运动的规律,结合牛顿第二定律和运动学公式进行求解.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案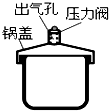 如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )
如图为某压力锅的结构简图.将压力阀套在出气孔上,给压力锅加热,在气体把压力阀顶起之前,锅内气体 ( )| A. | 压强增大 | B. | 内能不变 | ||
| C. | 对外界做正功 | D. | 分子平均动能增大 | ||
| E. | 对外没有做功 |
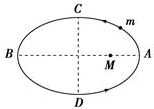
| A. | 速度最大点是A点 | B. | 速度最小点是C点 | ||
| C. | m从A 到B做加速运动 | D. | m从B 到A做加速运动 |
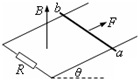 如图所示,两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有电阻R,导轨自身的电阻不计,磁场方向垂直于斜面向上,质量为m、电阻不计的金属棒ab在沿着斜面、与棒垂直的恒力F作用下沿导轨匀速上滑h高度,在此过程中( )
如图所示,两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有电阻R,导轨自身的电阻不计,磁场方向垂直于斜面向上,质量为m、电阻不计的金属棒ab在沿着斜面、与棒垂直的恒力F作用下沿导轨匀速上滑h高度,在此过程中( )| A. | 作用于金属棒上的各个力的合力所做的功等于零 | |
| B. | 作用于金属棒上的各个力的合力所做的功等于mgh与电阻R上发出的焦耳热之和 | |
| C. | 恒力F与安培力的合力所的功等于零 | |
| D. | 恒力F与安培力的合力所做的功等于电阻R上发出的焦耳热 |
| A. | 能就是功,功就是能 | |
| B. | 做功越多,物体的能就越大 | |
| C. | 能量转化的多少可以用功来量度 | |
| D. | 外力对物体不做功,这个物体就没有能量 |
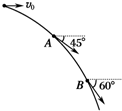 如图所示,一小球以v0=10m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2),以下判断中正确的是( )
如图所示,一小球以v0=10m/s的速度水平抛出,在落地之前经过空中A、B两点,在A点小球速度方向与水平方向的夹角为45°,在B点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计,g取10m/s2),以下判断中正确的是( )| A. | 经过A、B两点间的时间t=($\sqrt{3}$-1)s | B. | 经过A、B两点间的时间t=$\sqrt{3}$ s | ||
| C. | A、B两点间的高度差h=100 m | D. | A、B两点间的高度差h=15 m |
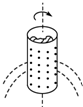
| A. | 水会从桶中甩出是因为水滴受到的力突然消失了 | |
| B. | 水会从桶中甩出是因为水滴受到向心力很大的缘故 | |
| C. | 加快脱水桶转动角速度,脱水效果会更好 | |
| D. | 这是一种离心现象的应用 |
| A. | 同时达到最大 | |
| B. | 还没有达到最大值 | |
| C. | 在没有达到额定功率前已经达到最大值 | |
| D. | 将在以后的过程中保持不变 |