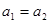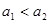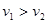题目内容
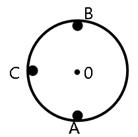
如图所示,AB为光滑竖直杆,ACB为构成直角的光滑L形直轨道,C处有一小圆弧连接可使小球顺利转弯(即通过转弯处不损失机械能)。套在AB杆上的小球自A点静止释放,分别沿AB轨道和ACB轨道运动,如果沿ACB轨道运动的时间是沿AB轨道运动时间的1.5倍,则BA与CA的夹角为:( )
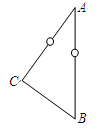

| A.30º | B.45º | C.53º | D.60º |
C
试题分析:设AB的长度为2L,小球沿AB做自由落体运动,运动的时间t2满足:
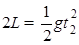
可解得
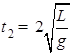 ,小球沿AC段运动时,a=gcosα,且AC=2Lcosα,所需的时间tAC满足;2Lcosα=
,小球沿AC段运动时,a=gcosα,且AC=2Lcosα,所需的时间tAC满足;2Lcosα=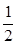 gcosα?t2AC, 解得:
gcosα?t2AC, 解得: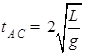
在C点小球的速度v=atAC,以后沿BC做匀加速运动,其加速度为:a'=gsinα,且BC=2Lsinα
故:2Lsinα=vtBC+
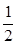 a′t2CB, 其中tBC=1.5t2-tAC=0.5t2=
a′t2CB, 其中tBC=1.5t2-tAC=0.5t2=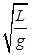
代入后解得:tanα=
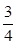 ,即α=53°,选项C 正确。
,即α=53°,选项C 正确。
练习册系列答案
相关题目
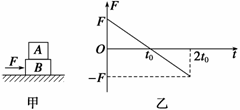
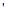 ,发现A、B-起以加速度a
,发现A、B-起以加速度a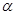 角,则:
角,则:


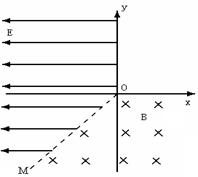
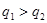 。当-q1、-q2经过P点时速度大小分别为v1、v2,加速度大小分别为a1、a2,下列关系式正确的是
。当-q1、-q2经过P点时速度大小分别为v1、v2,加速度大小分别为a1、a2,下列关系式正确的是