题目内容
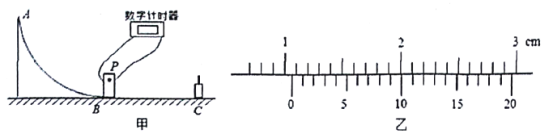
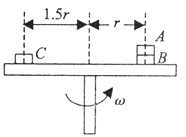
【题目】如图所示,叠放在水平转台上的物体A、B、C能随转台一起以角速度ω匀速转动,A、B、C的质量分别为mA、mB、mC,A与B、B与转台、C与转台间的动摩擦因数分别为μ1、μ2、μ3,A和B、C离转台中心的距离分别为r、1.5r.,最大静摩擦力等于滑动摩擦力。以下说法正确的是
A. B受A的摩擦力方向沿半径指向圆心
B. 随着角速度缓慢增大,C与转动相对滑动的临界条件为: ![]()
C. 若μ1=μ2=μ3,在转台角速度逐渐增大过程中,C先相对转台滑动
D. 若mA=mB=mC,当转台角速度增至某一值时,三个物体均刚好要滑动,那么μ1 :μ2 :μ3=1 :2 :3
【答案】C
【解析】A满足
A所受的向心力由B给A的静摩擦力提供,其方向指向圆心,则A给B的静摩擦力方向沿半径背离圆心,选项A错误;C将要滑动时,满足![]() ,解得
,解得![]() ,选项B错误;根据μmg=mRω2得,临界角速度
,选项B错误;根据μmg=mRω2得,临界角速度![]() ,C的半径大,当角速度增大时,C先达到最大静摩擦力,C最先滑动,故C正确.若mA=mB=mC,当转台角速度增至某一值时ω0,三个物体均刚好要滑动时,对C满足μ3mg=m1.5rω02;对A满足μ1mg=mrω02;对B满足μ22mg-μ1mg=mrω02;联立解得μ1 :μ2 :μ3=2 :2 :3,选项D错误;故选C.
,C的半径大,当角速度增大时,C先达到最大静摩擦力,C最先滑动,故C正确.若mA=mB=mC,当转台角速度增至某一值时ω0,三个物体均刚好要滑动时,对C满足μ3mg=m1.5rω02;对A满足μ1mg=mrω02;对B满足μ22mg-μ1mg=mrω02;联立解得μ1 :μ2 :μ3=2 :2 :3,选项D错误;故选C.

练习册系列答案
相关题目