��Ŀ����
B����ѡ��ģ��3-4��
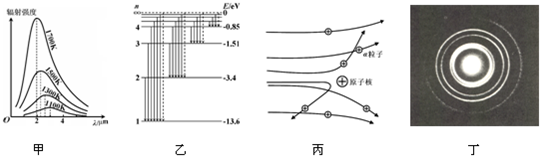
��1������˵������ȷ����
A�����ƫ������˵������һ���ݲ�
B���������Ϊ�ռ��ʱ�������ʵ��˶�״̬��
C�����˹ΤԤ�Բ���ʵ����֤�˵�Ų��Ĵ���
D���ڹ��˫�����ʵ���У���������������̹��Ϊ��⣬�����Ƽ����
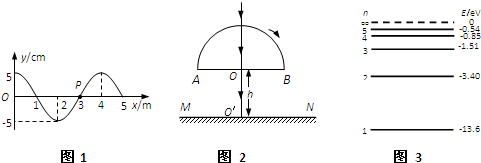
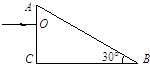
��2��ֱ�Dz������⾵�Ľ�����ͼ��ʾ��һ�����ߴ�AB�����䣬abΪ��������ߣ�ab��AB��ļнǦ�=60�㣮��֪���ֲ�����������n=
����
������������AB���ϵ������Ϊ ��
��ͼ�й���ab ����ܡ����ܡ�����AC�������ȥ��
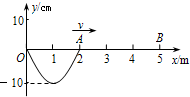
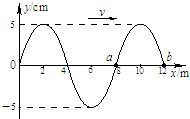
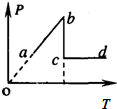
��3����ͼ��ʾ��һ����x���������ļ�г�Შ��t=0ʱ�̵IJ���ͼ����֪���Ĵ����ٶ�v=2m/s���Իش��������⣺
��д��x=0.5m�����ʵ�����г�˶��ı���ʽ�� cm��
��x=0.5m���ʵ���0��5.5s��ͨ����·��Ϊ cm��

��1������˵������ȷ����
A�����ƫ������˵������һ���ݲ�
B���������Ϊ�ռ��ʱ�������ʵ��˶�״̬��
C�����˹ΤԤ�Բ���ʵ����֤�˵�Ų��Ĵ���
D���ڹ��˫�����ʵ���У���������������̹��Ϊ��⣬�����Ƽ����
��2��ֱ�Dz������⾵�Ľ�����ͼ��ʾ��һ�����ߴ�AB�����䣬abΪ��������ߣ�ab��AB��ļнǦ�=60�㣮��֪���ֲ�����������n=
| 2 |
������������AB���ϵ������Ϊ
��ͼ�й���ab
��3����ͼ��ʾ��һ����x���������ļ�г�Შ��t=0ʱ�̵IJ���ͼ����֪���Ĵ����ٶ�v=2m/s���Իش��������⣺
��д��x=0.5m�����ʵ�����г�˶��ı���ʽ��
��x=0.5m���ʵ���0��5.5s��ͨ����·��Ϊ

��������1��ƫ������˵������һ�ֺᲨ���������Ϊ�ռ��ʱ�������ʵ��˶�״̬�йأ����˹ΤԤ�Ե�Ų��Ĵ��ڣ�����֤ʵ�˵�Ų����ڣ�����˫��������Ƶļ�ʽ�жϼ��ı仯��
��2���������䶨���������ǵĴ�С��ͨ����AC�������Ǻ��ٽ�DZȽϣ��ж��Ƿ���ȫ���䣮
��3�����ݲ����Ͳ�������������ڣ��Ӷ��ó��ʵ�������ڣ��ó��ʵ�����̣�����һ���������߹���·�̵���4�����������ʵ��·�̣�
��2���������䶨���������ǵĴ�С��ͨ����AC�������Ǻ��ٽ�DZȽϣ��ж��Ƿ���ȫ���䣮
��3�����ݲ����Ͳ�������������ڣ��Ӷ��ó��ʵ�������ڣ��ó��ʵ�����̣�����һ���������߹���·�̵���4�����������ʵ��·�̣�
����⣺��1��A�����ƫ������˵������һ�ֺᲨ����A����
B���������Ϊ�ռ��ʱ�������ʵ��˶�״̬�йأ���B����
C�����˹ΤԤ���˵�Ų��Ĵ��ڣ�����֤ʵ�˵�Ų��Ĵ��ڣ���C����
D��������x=
��֪�����IJ��������̹�IJ�������������ĸ������Ƽ�������D��ȷ��
��2���ٸ��ݼ��ι�ϵ֪�������Ϊ30�㣬�������䶨�ɵã�n=
�������Ǧ�=45�㣮
�ڹ���AC���ϵ������Ϊ60�㣬��Ϊsin60����sinC=
������ȫ���䣬���߲��ܴ�AC���������ȥ��
��3���ʵ�������ڵ��ڲ������ڣ�T=
=
s=1s����=
=2����x=0.5m�����ʵ���t=0ʱ�̴����������λ�ƴ���������Ϊy=Acos��t=5cos2��t cm��
�ʵ���һ���������߹���·�̵���4���������s=
��4A=
��4��5cm=110cm��
�ʴ�Ϊ����1��D ��2����45�� �ڲ��� ��3����y=5cos2��t 110cm
B���������Ϊ�ռ��ʱ�������ʵ��˶�״̬�йأ���B����
C�����˹ΤԤ���˵�Ų��Ĵ��ڣ�����֤ʵ�˵�Ų��Ĵ��ڣ���C����
D��������x=
| L |
| d |
��2���ٸ��ݼ��ι�ϵ֪�������Ϊ30�㣬�������䶨�ɵã�n=
| sin�� |
| sin30�� |
�������Ǧ�=45�㣮
�ڹ���AC���ϵ������Ϊ60�㣬��Ϊsin60����sinC=
| ||
| 2 |
��3���ʵ�������ڵ��ڲ������ڣ�T=
| �� |
| v |
| 2 |
| 2 |
| 2�� |
| T |
�ʵ���һ���������߹���·�̵���4���������s=
| t |
| T |
| 5.5 |
| 1 |
�ʴ�Ϊ����1��D ��2����45�� �ڲ��� ��3����y=5cos2��t 110cm
���������⿼���˲����������䶨�ɡ����桢ƫ������۵�֪ʶ�㣬�ѶȲ��ؼ�Ҫ��Ϥ�̲ģ��μ���Щ��������ͻ������ɣ�

��ϰ��ϵ�д�
�����Ŀ
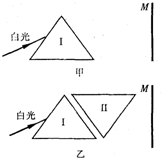 A����M���϶��·ֲ���ɫ��IJ�����С����
A����M���϶��·ֲ���ɫ��IJ�����С����