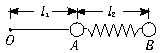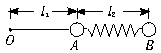题目内容
两只小球A和B用长为8m不可伸长的细线相连,B球质量是A球的3倍,两球位于离地面30.8m的空中.现先由静止释放小球A,0.8s后再由同一位置由静止释放小球B,不计空气阻力,重力加速度g取10m/s2.试求:(1)释放B球后,经过多长时间线将绷紧;
(2)A球在空中运动的时间(线绷紧时间极短,球落地后不再弹起).
【答案】分析:(1)根据位移时间公式,结合位移之差等于8m求出细线绷紧所需的时间.
(2)根据速度时间公式求出细线绷紧前瞬间A、B两球的速度,根据动量守恒定律求出绷紧后瞬间的速度.结合运动学公式求出A球在空中运动的总时间.
解答:解:(1)B运动时间t1线绷紧,此时,A已运动t1+0.8s,由运动学公式有
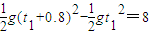 ,解得:t1=0.6s
,解得:t1=0.6s
(2)线绷紧前时刻,A速度为v1,B速度为v2,绷紧后共同速度为v,则
v1=g(t1+0.8)=14m/s,v2=gt1=6m/s,
mAv1+mBv2=(mA+mB)v,mB=3mA,
解得:v=8m/s,
此时A球已下落s1,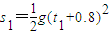 =9.8m
=9.8m
以后A和B一起以加速度g匀加速下落,又经时间t2,A落地,
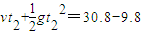
解得:t2=1.4s
A在空中运动总时间t=0.8s+0.6s+1.4s=2.8s.
答:(1)释放B球后,经过0.6s时间线将绷紧.
(2)A球在空中运动的时间为2.8s.
点评:本题综合考查了动量守恒定律、运动学公式,关键理清运动过程,结合运动学公式灵活求解.
(2)根据速度时间公式求出细线绷紧前瞬间A、B两球的速度,根据动量守恒定律求出绷紧后瞬间的速度.结合运动学公式求出A球在空中运动的总时间.
解答:解:(1)B运动时间t1线绷紧,此时,A已运动t1+0.8s,由运动学公式有
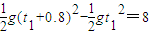 ,解得:t1=0.6s
,解得:t1=0.6s(2)线绷紧前时刻,A速度为v1,B速度为v2,绷紧后共同速度为v,则
v1=g(t1+0.8)=14m/s,v2=gt1=6m/s,
mAv1+mBv2=(mA+mB)v,mB=3mA,
解得:v=8m/s,
此时A球已下落s1,
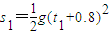 =9.8m
=9.8m以后A和B一起以加速度g匀加速下落,又经时间t2,A落地,
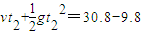
解得:t2=1.4s
A在空中运动总时间t=0.8s+0.6s+1.4s=2.8s.
答:(1)释放B球后,经过0.6s时间线将绷紧.
(2)A球在空中运动的时间为2.8s.
点评:本题综合考查了动量守恒定律、运动学公式,关键理清运动过程,结合运动学公式灵活求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目