题目内容
（8分）如图所示，空间存在着电场强度E＝2.5×102 N/C、方向竖直向上的匀强电场，在电场内一长为L＝0.5 m的绝缘细线一端固定于O点，另一端拴着质量m＝0.5 kg电荷量q＝4×10－2 C的小球。现将细线拉至水平位置，将小球由静止释放，当小球运动到最高点时细线受到的拉力恰好达到它能承受的最大值而断裂。取g＝10 m/s2。求：
(1)小球的电性；
(2)细线能承受的最大拉力值。
【答案】
（1）小球应带正电 （2）15N
【解析】
试题分析：（1）当小球运动到最高点时细线受到的拉力恰好达到它能承受的最大值而断开，知电场力的方向向上，小球应带正电．
（2）由动能定理得，(qE−mg)L＝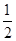
mv02 ①
在最高点：T−(qE−mg)＝m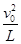 
②
由①②解得：T=3（qE-mg）=15N．
考点：本题考查动能定理和牛顿第二定律的综合运用
练习册系列答案
相关题目
如图所示，空间存在着强度E=2.5×102N/C方向竖直向上的匀强电场，在电场内一长为L=0.5m的绝缘细线，一端固定在O点，一端拴着质量m=0.5kg、电荷量q=4×10-2C的小球．现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂．取g=10m/s2．求：
如图所示，空间存在着由匀强磁场B和匀强电场E组成的正交电磁场，电场方向水平向左，磁场方向垂直纸面向里．有一带负电荷的小球P，从正交电磁场上方的某处自由落下，那么带电小球在通过正交电磁场时（ ）
（2013?顺义区一模）如图所示，空间存在着垂直纸面向外的水平的匀强磁场和竖直向上的匀强电场，磁感应强度为B，电场强度为E．在这个场区内，有一带正电的液滴a在电场力和重力作用下处于静止状态．现从场中某点由静止释放一个带负电的液滴bb（图中未画出），当它的运动方向变成水平方向时恰与a相撞，撞后两液滴合为一体，并沿水平方向做匀速直线运动．已知液滴b的质量是a质量的2倍，b所带的电量的绝对值是a所带电量大小的4倍，设相撞前a、b之间的静电力可不计．求：
如图所示，空间存在着与圆台母线垂直向外的磁场，各处的磁感应强度大小均为B，圆台母线与竖直方向的夹角为θ．一个质量为m、半径为r的匀质金属环位于圆台底部．环中通以恒定的电流I后圆环由静止向上运动，经过时间t后撤去该恒定电流并保持圆环闭合，圆环上升的最大高度为H．已知重力加速度为g，磁场的范围足够大．在圆环向上运动的过程中，下列说法正确的是（ ）