题目内容
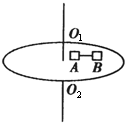 如图所示,匀速转动的水平圆盘上放有质量均为m的小物体A、B,AB间用细线沿半径方向相连.它们到转轴的距离分别为RA=0.2m、RB=0.3m.A、B与盘面间的最大静摩擦力均为重力的0.4倍.g取10m/s2,试求:
如图所示,匀速转动的水平圆盘上放有质量均为m的小物体A、B,AB间用细线沿半径方向相连.它们到转轴的距离分别为RA=0.2m、RB=0.3m.A、B与盘面间的最大静摩擦力均为重力的0.4倍.g取10m/s2,试求:(1)当细线上开始出现张力时圆盘的角速度ω0
(2)当A开始滑动时圆盘的角速度ω;
(3)在A即将滑动时,烧断细线,A、B将分别做什么运动?
分析:(1)由题意可知B与盘间已达的最大静摩擦力,故静摩擦力充当向心力,由向心力公式可求得角速度;
(2)A开始滑动时,说明A已达到最大静摩擦力,由向心力公式可求得角速度;
(3)由两物体的受力情况可知细线烧断后外力能否充当向心力,则可判断物体的运动.
(2)A开始滑动时,说明A已达到最大静摩擦力,由向心力公式可求得角速度;
(3)由两物体的受力情况可知细线烧断后外力能否充当向心力,则可判断物体的运动.
解答:解:(1)当细线上开始出现张力时,表明B与盘间的静摩擦力已达最大,则:μmg=mω02RB ①
解得:
ω0=
=3.65rad/s ②
圆盘的角速度为3.65rad/s
(2)当A开始滑动时,表明A与盘间的静摩擦力也已达最大,则:
对A:μmg-FT=m?2RA ③
对B:FT+μmg=mω2RB ④
由③④两式联解得:此时圆盘的角速度为:
ω=4rad/s ⑤
A开始滑动时圆盘的角速度为4rad/s
(3)烧断细线,A与盘间静摩擦力减小,继续随盘做半径为RA=20cm的圆周运动.而B由于最大静摩擦力不足以提供向心力而做离心运动.
故A继续做圆周运动,B做离心运动.
解得:
ω0=
|
圆盘的角速度为3.65rad/s
(2)当A开始滑动时,表明A与盘间的静摩擦力也已达最大,则:
对A:μmg-FT=m?2RA ③
对B:FT+μmg=mω2RB ④
由③④两式联解得:此时圆盘的角速度为:
ω=4rad/s ⑤
A开始滑动时圆盘的角速度为4rad/s
(3)烧断细线,A与盘间静摩擦力减小,继续随盘做半径为RA=20cm的圆周运动.而B由于最大静摩擦力不足以提供向心力而做离心运动.
故A继续做圆周运动,B做离心运动.
点评:本题考查圆周运动中力与运动的关系,注意本题中为静摩擦力与绳子的拉力充当向心力,故应注意静摩擦力是否已达到最大静摩擦力.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
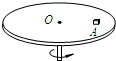 (2010?海淀区模拟)如图所示,匀速转动的水平圆盘上放置着一个物体A,物体距圆盘圆心O的距离为r,物体随着圆盘一起做匀速圆周运动,下列说法中正确的是( )
(2010?海淀区模拟)如图所示,匀速转动的水平圆盘上放置着一个物体A,物体距圆盘圆心O的距离为r,物体随着圆盘一起做匀速圆周运动,下列说法中正确的是( )