题目内容
1.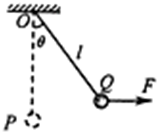 如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,初始时刻小球静止于P点,第一种情况是小球一直在水平拉力F1作用下,从P点缓慢地移动到Q点,至Q点时轻绳与竖直方向夹角为θ,张力大小为T1,第二种情况是小球一直在水平恒力F2作用下,从P点开始运动并恰好能到达Q点返回,至Q点时轻绳中的张力大小为T2,关于这两个过程,下列说法中正确的是(不计空气阻力,重力加速度为g)( )
如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,初始时刻小球静止于P点,第一种情况是小球一直在水平拉力F1作用下,从P点缓慢地移动到Q点,至Q点时轻绳与竖直方向夹角为θ,张力大小为T1,第二种情况是小球一直在水平恒力F2作用下,从P点开始运动并恰好能到达Q点返回,至Q点时轻绳中的张力大小为T2,关于这两个过程,下列说法中正确的是(不计空气阻力,重力加速度为g)( )| A. | 小球在第一种情况下从P运动到Q的过程中,水平拉力F1做的功为F1lsinθ | |
| B. | 小球在两种情况下从P运动到Q的过程中,轻绳的张力均一直变大 | |
| C. | T1=$\frac{mg}{cosθ}$,T2=mg | |
| D. | 小球在水平恒力F2作用下到达Q点后将会再次返回到P点 |
分析 第一次小球在水平拉力F作用下,从P点缓慢地移动到Q点,则小球处于平衡状态,第二次在水平恒力F′作用下,从P点开始运动并恰好能到达Q点,则到达Q点时速度为零,由于重力和拉力都是恒力,可以把这两个力合成为新的“重力”,则第二次小球的运动可以等效于单摆运动,找出“最低点”,最低点的速度最大,在Q点速度为零,则向心力为零,判断T2与mg的关系.
解答 解:A、第一种情况下,小球缓慢匀速运动,拉力F为变力,故不能根据恒力的功的计算方法求解;故A错误;
B、第一次运动过程中,根据几何关系可知,绳子的拉力${T}_{\;}=\frac{mg}{cosθ}$,所以轻绳的张力变大,
第二次由于重力和拉力都是恒力,可以把这两个力合成为新的“重力”,则第二次小球的运动可以等效于单摆运动,当绳子方向与重力和F′方向在同一直线上时,小球处于“最低点”,最低点的速度最大,此时绳子张力最大,所以第二次绳子张力先增大,后减小,故B错误;
C、第一次运动到Q点时,受力平衡,根据几何关系可知,${T}_{1}=\frac{mg}{cosθ}$,第二次运动到Q点时,速度为零,则向心力为零,则绳子拉力T2=mgcosθ+F′sinθ=mgcosθ+$\frac{mg(1-cosθ)}{sinθ}•sinθ$=mg,故C正确;
D、小球在水平恒力F2作用下到达Q点后将,松手后物体将在重力绳子的拉力作用下回到P点;故D正确;
故选:CD.
点评 本题的难点在第二次拉动小球运动过程的处理,由于重力和拉力都是恒力,可以把这两个力合成为新的“重力”,则第二次小球的运动可以等效于单摆运动,根据单摆的知识求解,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知火星是类地行星,质量和半径都比地球小,火星的质量是地球质量的$\frac{1}{q}$倍,半径是地球半径的$\frac{1}{p}$倍.如果有一天地球上的人类能在火星和地球之间通过航天器往来,根据以上信息,请你判断下列说法正确的是( )
| A. | 火星的同步卫星周期一定小于地球的同步卫星周期 | |
| B. | 某物体在该外星球表面上所受重力是它在地球表面上所受重力的$\frac{p}{q}$倍 | |
| C. | 火星上第一宇宙速度是地球上第一宇宙速度的$\sqrt{\frac{p}{q}}$倍 | |
| D. | 从地球上发射航天器到火星上去,发射速度应不小于16.7km/s |
6. 如图所示,三条平行且等间距的虚线表示电场中的三个等势面,其电势分别为10V、20V、30V.实线是一带电的粒子(不计重力)在该区域内运动的轨迹,对于轨迹上的a、b、c三点,已知:带电粒子带电量为0.01C,在a点处的动能为0.5J,则该带电粒子( )
如图所示,三条平行且等间距的虚线表示电场中的三个等势面,其电势分别为10V、20V、30V.实线是一带电的粒子(不计重力)在该区域内运动的轨迹,对于轨迹上的a、b、c三点,已知:带电粒子带电量为0.01C,在a点处的动能为0.5J,则该带电粒子( )
 如图所示,三条平行且等间距的虚线表示电场中的三个等势面,其电势分别为10V、20V、30V.实线是一带电的粒子(不计重力)在该区域内运动的轨迹,对于轨迹上的a、b、c三点,已知:带电粒子带电量为0.01C,在a点处的动能为0.5J,则该带电粒子( )
如图所示,三条平行且等间距的虚线表示电场中的三个等势面,其电势分别为10V、20V、30V.实线是一带电的粒子(不计重力)在该区域内运动的轨迹,对于轨迹上的a、b、c三点,已知:带电粒子带电量为0.01C,在a点处的动能为0.5J,则该带电粒子( )| A. | 可能是带负电 | B. | 在b点处的电势能为0.5J | ||
| C. | 在b点处的动能为零 | D. | 在c点处的动能为0.4 J |
11.由电场强度的定义式可知,在电场中的同一点有( )
| A. | 电场强度E跟F成正比,跟q成反比 | |
| B. | 无论试探电荷q的值如何变化,F与q的比值始终不变 | |
| C. | 电场中某点的场强为零,则处在该点的电荷受到的电场力不一定为零 | |
| D. | 一个不带电的小球在P点受到的电场力为零,则P点的场强一定为零 |

 ”型金属细框竖直放置在两水银槽中,“
”型金属细框竖直放置在两水银槽中,“



