题目内容
如图所示，A为带正电Q的金属板．小球的质量为m、电荷量为q，用绝缘丝线悬挂于O点，受水平向右的电场力偏转θ角后静止．小球静止时的位置沿金属板的垂直平分线，且距板为r处．试求小球所在处的电场强度．分析：以小球为研究对象，分析受力情况，作出力图，小球处于静止状态，合力为零，根据平衡条件和电场力公式F=qE，结合求解电场强度E．
解答：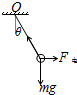
解：小球的受力如图所示．由平衡条件得：
F电=mgtanθ
又F电=qE
解得，小球所在处的电场强度：E=
小球带正电荷，电场强度方向与其受到的电场力方向一致，方向水平向右．
答：小球所在处的电场强度大小为
，方向水平向右．
解：小球的受力如图所示．由平衡条件得：F电=mgtanθ
又F电=qE
解得，小球所在处的电场强度：E=
| mgtanθ |
| q |
小球带正电荷，电场强度方向与其受到的电场力方向一致，方向水平向右．
答：小球所在处的电场强度大小为
| mgtanθ |
| q |
点评：本题是带电体在复合场中平衡问题，分析受力是关键，同时要掌握场强与电场力方向的关系．
练习册系列答案
相关题目
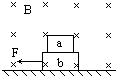如图所示，a为带正电的小物块，b是一不带电的绝缘物块，a、b叠放与粗糙的水平地面上，地面上方有垂直纸面向里的匀强磁场，现用水平恒力F拉b物块，使a、b一起无相对滑动地向左加速运动，在加速运动阶段（ ）
如图所示，a为带正电的小物块，b是一不带电的绝缘物块，a、b叠放于粗糙的水平地面上，地面上方有垂直纸面向里的匀强磁场，现用水平恒力F拉b物块，使a、b一起无相对滑动地向左加速运动，在加速运动阶段（ ）
（2003?顺德区模拟）如图所示，a为带正电的物体，b为不带电的绝缘物块，a、b叠放在粗糙水平地面上．地面上方有垂直纸面向里的匀强磁场，现用恒力F拉b，使a、b一起无相对滑动地向左加速运动，则在加速阶段，a受到b施加的摩擦力方向及大小变化是（ ）
如图所示，A为带正电的点电荷，电量为Q，中间竖直放置一无限大的金属板，B为质量为m、电量为+q的小球，用绝缘线悬挂于O点，平衡时丝线与竖直方向的夹角为θ，且A、B二个小球在同一水平面上，间距为L，则金属板的感应电荷在小球B处产生的电场强度大小E为（ ）A、E=
| ||||
B、E=
| ||||
C、E=
| ||||
D、E=
|