题目内容
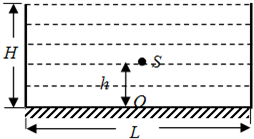 如图所示,高度为H=1m圆柱形容器中盛满折射率n=2的某种透明液体,容器底部安装一块平面镜,容器直径L=2H,在圆心O点正上方h高度处有一点光源S.
如图所示,高度为H=1m圆柱形容器中盛满折射率n=2的某种透明液体,容器底部安装一块平面镜,容器直径L=2H,在圆心O点正上方h高度处有一点光源S.①点光源S发出的光在水中传播的速度为多少?
②从液体上方观察要使S发出的光照亮整个液体表面,h应该满足什么条件?(已知sin37°=0.6)
分析:①点光源S发出的光在水中传播的速度由公式v=
求解,c是真空中的光速,c=3×108m/s.
②要使人从液体表面上任意位置处能够观察到点光源S发出的光,点光源发出的光必须全部能折射进入空气中,根据对称性,作出点光源经平面镜所成的像.当光射向水面时,入射角应不大于临界角,光线才能射入空气中.由几何知识求出h应满足的条件.
| c |
| n |
②要使人从液体表面上任意位置处能够观察到点光源S发出的光,点光源发出的光必须全部能折射进入空气中,根据对称性,作出点光源经平面镜所成的像.当光射向水面时,入射角应不大于临界角,光线才能射入空气中.由几何知识求出h应满足的条件.
解答: 解:(1)由n=
解:(1)由n=
得,点光源S发出的光在水中传播的速度:v=
=
=1.5×108m/s;
(2)点光源S通过平面镜所成像为S′,如图所示,如果反射光线能照亮全部液面则入射角应满足i≤C,C为全反射临界角.
由 sinC=
,C=30°
tani=
≤tanC,L=2H
解得:h≥(
-1)H=(
-1)m
又h<H=1m
所以h应该满足的条件是:(
-1)m≤h<1m
答:
①点光源S发出的光在水中传播的速度为1.5×108m/s;
②从液体上方观察要使S发出的光照亮整个液体表面,h应该满足的条件是:(
-1)m≤h<1m.
 解:(1)由n=
解:(1)由n=| c |
| v |
| c |
| n |
| 3×108 |
| 2 |
(2)点光源S通过平面镜所成像为S′,如图所示,如果反射光线能照亮全部液面则入射角应满足i≤C,C为全反射临界角.
由 sinC=
| 1 |
| n |
tani=
| L |
| 2(H+h) |
解得:h≥(
| 3 |
| 3 |
又h<H=1m
所以h应该满足的条件是:(
| 3 |
答:
①点光源S发出的光在水中传播的速度为1.5×108m/s;
②从液体上方观察要使S发出的光照亮整个液体表面,h应该满足的条件是:(
| 3 |
点评:本题要利用对称性作出平面镜所成的像,点光源发出的光好像从虚像发出的.再根据临界角和几何知识求解h满足的条件.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【物理——选修3—4】(15分)
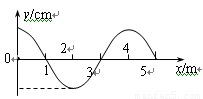
(1)(5分)振源以原点O为平衡位置,沿y轴方向做简谐运动,它发出的简谐波在x轴上以v=2m/s沿正方向传播,在某一时刻的波形如图所示。在原点的右方有一质元P从图示时刻开始,经过0.5s在x轴下方且向上运动,则质元P所在的位置可能是 。
| A.0.5 m |
| B.1.5m |
| C.2.5 m |
| D.3.5m |
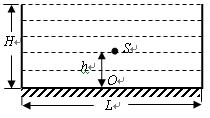
①点光源S发出的光在水中传播的速度为多少?
②从液体上方观察要使S发出的光照亮整个液体表面,h应该满足什么条件?(已知
 )
)
 gsinθ·t2,由此可求得落地的时间t.
gsinθ·t2,由此可求得落地的时间t.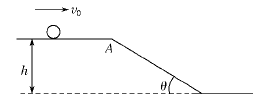
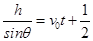 gsinθ·t2,由此可求得落地的时间t.
gsinθ·t2,由此可求得落地的时间t.
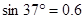 )
)