题目内容
17. 如图所示,质量相同的三颗卫星a、b、c绕地球做匀速圆周运动,其中b、c在地球的同步轨道上,a距离地球表面的高度为R,此时a、b恰好相距最近.已知地球质量为M、半径为R、地球自转的角速度为ω.万有引力常量为G,则( )
如图所示,质量相同的三颗卫星a、b、c绕地球做匀速圆周运动,其中b、c在地球的同步轨道上,a距离地球表面的高度为R,此时a、b恰好相距最近.已知地球质量为M、半径为R、地球自转的角速度为ω.万有引力常量为G,则( )| A. | 发射卫星b时速度要大于7.9km/s | |
| B. | 若要卫星c与b实现对接,可让卫星c加速 | |
| C. | 卫星b距离地面的高度为$\root{3}{\frac{GM}{{ω}^{2}}}$ | |
| D. | 卫星a和b下一次相距最近还需经过的时间t=$\frac{2π}{\sqrt{\frac{GM}{8{R}^{3}}-ω}}$ |
分析 第一宇宙速度7.9km/s是指在地球上发射的物体绕地球飞行作圆周运动所需的最小初始速度,第二宇宙速度11.2km/s是物体挣脱地球引力束缚的最小发射速度.
卫星从低轨道到高轨道需要克服引力做较多的功.b、c在地球的同步轨道上,所以卫星b、c和地球具有相同的周期和角速度.
解答 解:A、卫星b绕地球做匀速圆周运动,7.9km/s是指在地球上发射的物体绕地球飞行作圆周运动所需的最小初始速度,所以发射卫星b时速度大于7.9km/s,故A正确;
B、让卫星c加速,所需的向心力增大,由于万有引力小于所需的向心力,卫星c会做离心运动,离开原轨道,所以不能与b实现对接.故B错误;
C、b、c在地球的同步轨道上,所以卫星b、c和地球具有相同的周期和角速度.
由万有引力提供向心力,即$\frac{GMm}{{r}^{2}}$=mω2r
得:r=$\root{3}{\frac{GM}{{ω}^{2}}}$.所以卫星b距离地面的高度为$\root{3}{\frac{GM}{{ω}^{2}}}$-R:故C错误;
D、b与c的角速度:ω=$\sqrt{\frac{GM}{{r}^{3}}}$
a距离地球表面的高度为R,所以卫星a的角速度ωa=$\sqrt{\frac{GM}{{8R}^{3}}}$
此时a、b恰好相距最近,到卫星a和b下一次相距最近,
(ωa-ω)t=2π
t=$\frac{2π}{\sqrt{\frac{g}{8R}}-ω}$,故D正确;
故选:AD.
点评 理解三种宇宙速度,特别注意第一宇宙速度的三种说法.能抓住万有引力提供向心力列出等式解决问题的思路,再进行讨论求解.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
8.在“探究求合力的方法”实验中,现有木板、白纸、图钉、橡皮筋、细绳套和一把弹簧秤.

(1)为完成实验,某同学另找来一根弹簧,先测量其劲度系数,得到的实验数据如表:
用作图法求得该弹簧的劲度系数k=55N/m;
(2)某次实验中,弹簧秤的指针位置如图2所示,其读数为2.10N.

(1)为完成实验,某同学另找来一根弹簧,先测量其劲度系数,得到的实验数据如表:
| 弹力F(N) | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 伸长量x(10-2m) | 0.74 | 1.80 | 2.80 | 3.72 | 4.60 | 5.58 | 6.42 |
(2)某次实验中,弹簧秤的指针位置如图2所示,其读数为2.10N.
5.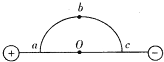 如图两等量异种点电荷,以两电荷连线的中点O为圆心画出半圆,在半圆上有a、b、c三点,a、c分别为半圆与两电荷连线的交点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )
如图两等量异种点电荷,以两电荷连线的中点O为圆心画出半圆,在半圆上有a、b、c三点,a、c分别为半圆与两电荷连线的交点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )
 如图两等量异种点电荷,以两电荷连线的中点O为圆心画出半圆,在半圆上有a、b、c三点,a、c分别为半圆与两电荷连线的交点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )
如图两等量异种点电荷,以两电荷连线的中点O为圆心画出半圆,在半圆上有a、b、c三点,a、c分别为半圆与两电荷连线的交点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )| A. | a、c两点的电场强度不相同 | |
| B. | a、c两点的电势相同 | |
| C. | 负电荷在a点的电势能大于在b点的电势能 | |
| D. | 将正电荷由c点移到b点电场力做负功 |



 如图所示,表面光滑的圆锥的锥角α=106°,圆锥顶端O点处固定了一根竖直杆.一根长10m的轻绳一端固定在竖直杆上,另一端连接质量为1.6kg的小球A.小球A静止时,轻绳与竖直杆的夹角β=37°.现在使小球A以1rad/s的角速度绕竖直杆匀速转动,重力加速度g取10m/s2,sin37°=0.6,sin53°=0.8,试求轻绳中的张力为多大?
如图所示,表面光滑的圆锥的锥角α=106°,圆锥顶端O点处固定了一根竖直杆.一根长10m的轻绳一端固定在竖直杆上,另一端连接质量为1.6kg的小球A.小球A静止时,轻绳与竖直杆的夹角β=37°.现在使小球A以1rad/s的角速度绕竖直杆匀速转动,重力加速度g取10m/s2,sin37°=0.6,sin53°=0.8,试求轻绳中的张力为多大?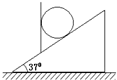 如图所示,一个质量m=10kg的光滑小球被竖直挡板挡在倾角为37°的斜面上,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
如图所示,一个质量m=10kg的光滑小球被竖直挡板挡在倾角为37°的斜面上,(sin37°=0.6,cos37°=0.8,g=10m/s2)求: