题目内容
【题目】如图所示为研究电子枪中电子在中场中运动的简化模型示意图。在xOy平面的ABCD区域内，存在两个大小均为E的匀强电场Ⅰ和Ⅱ，两电场的边界均是边长为L的正方形(不计粒子所受重力)。
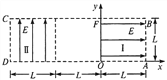
（1）在该区域AB边的中点处由静止释放电子，求电子离开ABCD区域的位置；
（2）在电场Ⅰ区域内适当位置由静止释放电子，电子恰能从ABCD区域左下角D处离开，求所有释放点的位置；
（3）若将左侧电场Ⅱ整体水平向右移动
，仍使电子从ABCD区域左下角D处离开(D不随电场移动)，求在电场Ⅰ区域内由静止释放电子的所有位置。
【答案】①
②
③
【解析】（1）设电子的质量为m，电量为e，在电场I中释放后将做出速度为零的匀加速直线运动，出区域I时的速度为vo，接着进入电场II做类平抛运动，假设电子从CD边射出，出射点纵坐标为y，对电子的整个运动过程运用动能定理和匀变速直线运动公式有：
eEL=
mv2，
在电场Ⅱ区域内的偏转，L=vt， 
，方向向下，
故： 
所以位置坐标（-2L， 
L）
（2）设释放位置坐标为（x1，y1），在电场I中电子被加速到v1，然后进入电场II做类平抛运动，并从D点离开，有：eEx1=
mv2，
L=vt， 
，所以满足
方程的点即为释放点的位置
（3）设释放位置坐标为（x2，y2），eEx2=
mv2，在电场I中加速到v2，进入电场II后做类平抛运动，在高度为y′处离开电场II时的情景与（2）中类似，然后电子做匀速直线运动，经过D点，则有：L=vt1， 
， 
， 
， 
，
所以满足
方程的点即为释放点的位置．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
