题目内容
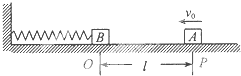
【题目】如图，轻弹簧的一端固定，另一端与滑块B相连，B静止在水平导轨上的O点，此时弹簧处于原长．另一质量与B相同的滑块A从导轨上的P点以初速度v0向B滑行，当A滑过距离l时，与B相碰．碰撞时间极短，碰后A、B粘在一起运动．设滑块A和B均可视为质点，与导轨的动摩擦因数均为μ．重力加速度为g．若A、B压缩弹簧后恰能返回到O点并停止，求弹簧的最大压缩量．
【答案】
【解析】
试题分析：设A、B质量均为m，A刚接触B时的速度为v1，碰后瞬间共同的速度为v2；
以A为研究对象，从P到O，由能量守恒定律得：μmgl=
mv02-
mv12，
以A、B为研究对象，碰撞瞬间系统动量守恒，以A的初速度方向为正方向，由动量守恒定律：
mv1=2mv2，
解得：
，
碰后A、B由O点向左运动，又返回到O点，设弹簧的最大压缩量为x，由能量守恒定律得：
μ（2mg）2x=
2mv22，
解得：．
练习册系列答案
相关题目
