题目内容

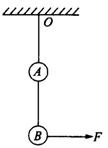
如图9所示，轻绳AB能承受的最大拉力为100N，在它下面悬挂一重为50N的重物，分两种情况缓慢地拉起重物．第一次，施加一水平方向的力F作用于轻绳AB的O点；第二次用拴有光滑小环的绳子，且绳子所能承受的最大拉力也为50N．绳子刚好断裂时，绳AB上部分与竖直方向的夹角分别为θ1和θ2，关于两者大小关系的说法中正确的是（　　）
分析：分别对O点受力分析，根据绳子拉力的最大值，分别求出绳AB上部分与竖直方向的夹角分别为θ1和θ2，从而比较出大小．
解答：解：第一次，绳子固定在O点，施加一水平方向的力F作用于绳子，受力如图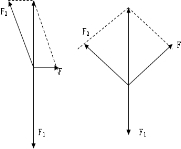，因为BO绳的拉力为50N，当水平绳的拉力为50N时，绳子刚好断裂，此时AO绳的拉力为50
2
N，小于100N，则绳AB上部分与竖直方向的夹角θ1=45°．
第二次用拴有光滑小环的绳子，因为F1=F2=50N，当F=50N时受力如图，绳刚好断裂，此时绳AB上部分与竖直方向的夹角θ2=60°．
所以θ1＜θ2．故C正确，A、B、D错误．
故选：C．
点评：解决本题的关键知道结点与圆环的区别，通过圆环的AB绳上拉力处处相等，通过结点O，0A绳和OB绳的拉力不等．
练习册系列答案
相关题目

第二部分  牛顿运动定律

第一讲 牛顿三定律

一、牛顿第一定律

1、定律。惯性的量度

2、观念意义，突破“初态困惑”

二、牛顿第二定律

1、定律

2、理解要点

a、矢量性

b、独立作用性：ΣF → a ，ΣFx → ax …

c、瞬时性。合力可突变，故加速度可突变（与之对比：速度和位移不可突变）；牛顿第二定律展示了加速度的决定式（加速度的定义式仅仅展示了加速度的“测量手段”）。

3、适用条件

a、宏观、低速

b、惯性系

对于非惯性系的定律修正——引入惯性力、参与受力分析

三、牛顿第三定律

1、定律

2、理解要点

a、同性质（但不同物体）

b、等时效（同增同减）

c、无条件（与运动状态、空间选择无关）

第二讲 牛顿定律的应用

一、牛顿第一、第二定律的应用

单独应用牛顿第一定律的物理问题比较少，一般是需要用其解决物理问题中的某一个环节。

应用要点：合力为零时，物体靠惯性维持原有运动状态；只有物体有加速度时才需要合力。有质量的物体才有惯性。a可以突变而v、s不可突变。

1、如图1所示，在马达的驱动下，皮带运输机上方的皮带以恒定的速度向右运动。现将一工件（大小不计）在皮带左端A点轻轻放下，则在此后的过程中（      ）

A、一段时间内，工件将在滑动摩擦力作用下，对地做加速运动

B、当工件的速度等于v时，它与皮带之间的摩擦力变为静摩擦力

C、当工件相对皮带静止时，它位于皮带上A点右侧的某一点

D、工件在皮带上有可能不存在与皮带相对静止的状态

解说：B选项需要用到牛顿第一定律，A、C、D选项用到牛顿第二定律。

较难突破的是A选项，在为什么不会“立即跟上皮带”的问题上，建议使用反证法（t → 0 ，a → ∞ ，则ΣFx → ∞ ，必然会出现“供不应求”的局面）和比较法（为什么人跳上速度不大的物体可以不发生相对滑动？因为人是可以形变、重心可以调节的特殊“物体”）

此外，本题的D选项还要用到匀变速运动规律。用匀变速运动规律和牛顿第二定律不难得出

只有当L ＞ 时（其中μ为工件与皮带之间的动摩擦因素），才有相对静止的过程，否则没有。

答案：A、D

思考：令L = 10m ，v = 2 m/s ，μ= 0.2 ，g取10 m/s2 ，试求工件到达皮带右端的时间t（过程略，答案为5.5s）

进阶练习：在上面“思考”题中，将工件给予一水平向右的初速v0 ，其它条件不变，再求t（学生分以下三组进行）——

① v0 = 1m/s  (答：0.5 + 37/8 = 5.13s)

② v0 = 4m/s  (答：1.0 + 3.5 = 4.5s)

③ v0 = 1m/s  (答：1.55s)

2、质量均为m的两只钩码A和B，用轻弹簧和轻绳连接，然后挂在天花板上，如图2所示。试问：

① 如果在P处剪断细绳，在剪断瞬时，B的加速度是多少？

② 如果在Q处剪断弹簧，在剪断瞬时，B的加速度又是多少？

解说：第①问是常规处理。由于“弹簧不会立即发生形变”，故剪断瞬间弹簧弹力维持原值，所以此时B钩码的加速度为零（A的加速度则为2g）。

第②问需要我们反省这样一个问题：“弹簧不会立即发生形变”的原因是什么？是A、B两物的惯性，且速度v和位移s不能突变。但在Q点剪断弹簧时，弹簧却是没有惯性的（没有质量），遵从理想模型的条件，弹簧应在一瞬间恢复原长！即弹簧弹力突变为零。

答案：0 ；g 。

二、牛顿第二定律的应用

应用要点：受力较少时，直接应用牛顿第二定律的“矢量性”解题。受力比较多时，结合正交分解与“独立作用性”解题。

在难度方面，“瞬时性”问题相对较大。

1、滑块在固定、光滑、倾角为θ的斜面上下滑，试求其加速度。

解说：受力分析 → 根据“矢量性”定合力方向 → 牛顿第二定律应用

答案：gsinθ。

思考：如果斜面解除固定，上表仍光滑，倾角仍为θ，要求滑块与斜面相对静止，斜面应具备一个多大的水平加速度？（解题思路完全相同，研究对象仍为滑块。但在第二环节上应注意区别。答：gtgθ。）

进阶练习1：在一向右运动的车厢中，用细绳悬挂的小球呈现如图3所示的稳定状态，试求车厢的加速度。（和“思考”题同理，答：gtgθ。）

进阶练习2、如图4所示，小车在倾角为α的斜面上匀加速运动，车厢顶用细绳悬挂一小球，发现悬绳与竖直方向形成一个稳定的夹角β。试求小车的加速度。

解：继续贯彻“矢量性”的应用，但数学处理复杂了一些（正弦定理解三角形）。

分析小球受力后，根据“矢量性”我们可以做如图5所示的平行四边形，并找到相应的夹角。设张力T与斜面方向的夹角为θ，则

θ=（90°+ α）- β= 90°-（β-α）                 （1）

对灰色三角形用正弦定理，有

 =                                        （2）

解（1）（2）两式得：ΣF = 

最后运用牛顿第二定律即可求小球加速度（即小车加速度）

答： 。

2、如图6所示，光滑斜面倾角为θ，在水平地面上加速运动。斜面上用一条与斜面平行的细绳系一质量为m的小球，当斜面加速度为a时（a＜ctgθ），小球能够保持相对斜面静止。试求此时绳子的张力T 。

解说：当力的个数较多，不能直接用平行四边形寻求合力时，宜用正交分解处理受力，在对应牛顿第二定律的“独立作用性”列方程。

正交坐标的选择，视解题方便程度而定。

解法一：先介绍一般的思路。沿加速度a方向建x轴，与a垂直的方向上建y轴，如图7所示（N为斜面支持力）。于是可得两方程

ΣFx = ma ，即Tx － Nx = ma

ΣFy = 0 ， 即Ty + Ny = mg

代入方位角θ，以上两式成为

T cosθ－N sinθ = ma                       （1）

T sinθ + Ncosθ = mg                       （2）

这是一个关于T和N的方程组，解（1）（2）两式得：T = mgsinθ + ma cosθ

解法二：下面尝试一下能否独立地解张力T 。将正交分解的坐标选择为：x——斜面方向，y——和斜面垂直的方向。这时，在分解受力时，只分解重力G就行了，但值得注意，加速度a不在任何一个坐标轴上，是需要分解的。矢量分解后，如图8所示。

根据独立作用性原理，ΣFx = max

即：T － Gx = max

即：T － mg sinθ = m acosθ

显然，独立解T值是成功的。结果与解法一相同。

答案：mgsinθ + ma cosθ

思考：当a＞ctgθ时，张力T的结果会变化吗？（从支持力的结果N = mgcosθ－ma sinθ看小球脱离斜面的条件，求脱离斜面后，θ条件已没有意义。答：T = m 。）

学生活动：用正交分解法解本节第2题“进阶练习2”

进阶练习：如图9所示，自动扶梯与地面的夹角为30°，但扶梯的台阶是水平的。当扶梯以a = 4m/s2的加速度向上运动时，站在扶梯上质量为60kg的人相对扶梯静止。重力加速度g = 10 m/s2，试求扶梯对人的静摩擦力f 。

解：这是一个展示独立作用性原理的经典例题，建议学生选择两种坐标（一种是沿a方向和垂直a方向，另一种是水平和竖直方向），对比解题过程，进而充分领会用牛顿第二定律解题的灵活性。

答：208N 。

3、如图10所示，甲图系着小球的是两根轻绳，乙图系着小球的是一根轻弹簧和轻绳，方位角θ已知。现将它们的水平绳剪断，试求：在剪断瞬间，两种情形下小球的瞬时加速度。

解说：第一步，阐明绳子弹力和弹簧弹力的区别。

（学生活动）思考：用竖直的绳和弹簧悬吊小球，并用竖直向下的力拉住小球静止，然后同时释放，会有什么现象？原因是什么？

结论——绳子的弹力可以突变而弹簧的弹力不能突变（胡克定律）。

第二步，在本例中，突破“绳子的拉力如何瞬时调节”这一难点（从即将开始的运动来反推）。

知识点，牛顿第二定律的瞬时性。

答案：a甲 = gsinθ ；a乙 = gtgθ 。

应用：如图11所示，吊篮P挂在天花板上，与吊篮质量相等的物体Q被固定在吊篮中的轻弹簧托住，当悬挂吊篮的细绳被烧断瞬间，P、Q的加速度分别是多少？

解：略。

答：2g ；0 。

三、牛顿第二、第三定律的应用

要点：在动力学问题中，如果遇到几个研究对象时，就会面临如何处理对象之间的力和对象与外界之间的力问题，这时有必要引进“系统”、“内力”和“外力”等概念，并适时地运用牛顿第三定律。

在方法的选择方面，则有“隔离法”和“整体法”。前者是根本，后者有局限，也有难度，但常常使解题过程简化，使过程的物理意义更加明晰。

对N个对象，有N个隔离方程和一个（可能的）整体方程，这（N + 1）个方程中必有一个是通解方程，如何取舍，视解题方便程度而定。

补充：当多个对象不具有共同的加速度时，一般来讲，整体法不可用，但也有一种特殊的“整体方程”，可以不受这个局限（可以介绍推导过程）——

Σ= m1 + m2 + m3 + … + mn

其中Σ只能是系统外力的矢量和，等式右边也是矢量相加。

1、如图12所示，光滑水平面上放着一个长为L的均质直棒，现给棒一个沿棒方向的、大小为F的水平恒力作用，则棒中各部位的张力T随图中x的关系怎样？

解说：截取隔离对象，列整体方程和隔离方程（隔离右段较好）。

答案：N = x 。

思考：如果水平面粗糙，结论又如何？

解：分两种情况，（1）能拉动；（2）不能拉动。

第（1）情况的计算和原题基本相同，只是多了一个摩擦力的处理，结论的化简也麻烦一些。

第（2）情况可设棒的总质量为M ，和水平面的摩擦因素为μ，而F = μMg ，其中l＜L ，则x＜(L-l)的右段没有张力，x＞(L-l)的左端才有张力。

答：若棒仍能被拉动，结论不变。

若棒不能被拉动，且F = μMg时（μ为棒与平面的摩擦因素，l为小于L的某一值，M为棒的总质量），当x＜(L-l)，N≡0 ；当x＞(L-l)，N = 〔x -〈L-l〉〕。

应用：如图13所示，在倾角为θ的固定斜面上，叠放着两个长方体滑块，它们的质量分别为m1和m2 ，它们之间的摩擦因素、和斜面的摩擦因素分别为μ1和μ2 ，系统释放后能够一起加速下滑，则它们之间的摩擦力大小为：

A、μ1 m1gcosθ ；    B、μ2 m1gcosθ ；

C、μ1 m2gcosθ ；    D、μ1 m2gcosθ ；

解：略。

答：B 。（方向沿斜面向上。）

思考：（1）如果两滑块不是下滑，而是以初速度v0一起上冲，以上结论会变吗？（2）如果斜面光滑，两滑块之间有没有摩擦力？（3）如果将下面的滑块换成如图14所示的盒子，上面的滑块换成小球，它们以初速度v0一起上冲，球应对盒子的哪一侧内壁有压力？

解：略。

答：（1）不会；（2）没有；（3）若斜面光滑，对两内壁均无压力，若斜面粗糙，对斜面上方的内壁有压力。

2、如图15所示，三个物体质量分别为m1 、m2和m3 ，带滑轮的物体放在光滑水平面上，滑轮和所有接触面的摩擦均不计，绳子的质量也不计，为使三个物体无相对滑动，水平推力F应为多少？

解说：

此题对象虽然有三个，但难度不大。隔离m2 ，竖直方向有一个平衡方程；隔离m1 ，水平方向有一个动力学方程；整体有一个动力学方程。就足以解题了。

答案：F =  。

思考：若将质量为m3物体右边挖成凹形，让m2可以自由摆动（而不与m3相碰），如图16所示，其它条件不变。是否可以选择一个恰当的F′，使三者无相对运动？如果没有，说明理由；如果有，求出这个F′的值。

解：此时，m2的隔离方程将较为复杂。设绳子张力为T ，m2的受力情况如图，隔离方程为：

 = m2a

隔离m1 ，仍有：T = m1a

解以上两式，可得：a = g

最后用整体法解F即可。

答：当m1 ≤ m2时，没有适应题意的F′；当m1 ＞ m2时，适应题意的F′=  。

3、一根质量为M的木棒，上端用细绳系在天花板上，棒上有一质量为m的猫，如图17所示。现将系木棒的绳子剪断，同时猫相对棒往上爬，但要求猫对地的高度不变，则棒的加速度将是多少？

解说：法一，隔离法。需要设出猫爪抓棒的力f ，然后列猫的平衡方程和棒的动力学方程，解方程组即可。

法二，“新整体法”。

据Σ= m1 + m2 + m3 + … + mn ，猫和棒的系统外力只有两者的重力，竖直向下，而猫的加速度a1 = 0 ，所以：

（ M + m ）g = m·0 + M a1 

解棒的加速度a1十分容易。

答案：g 。

四、特殊的连接体

当系统中各个体的加速度不相等时，经典的整体法不可用。如果各个体的加速度不在一条直线上，“新整体法”也将有一定的困难（矢量求和不易）。此时，我们回到隔离法，且要更加注意找各参量之间的联系。

解题思想：抓某个方向上加速度关系。方法：“微元法”先看位移关系，再推加速度关系。、

1、如图18所示，一质量为M 、倾角为θ的光滑斜面，放置在光滑的水平面上，另一个质量为m的滑块从斜面顶端释放，试求斜面的加速度。

解说：本题涉及两个物体，它们的加速度关系复杂，但在垂直斜面方向上，大小是相等的。对两者列隔离方程时，务必在这个方向上进行突破。

（学生活动）定型判断斜面的运动情况、滑块的运动情况。

位移矢量示意图如图19所示。根据运动学规律，加速度矢量a1和a2也具有这样的关系。

（学生活动）这两个加速度矢量有什么关系？

沿斜面方向、垂直斜面方向建x 、y坐标，可得：

a1y = a2y             ①

且：a1y = a2sinθ     ②

隔离滑块和斜面，受力图如图20所示。

对滑块，列y方向隔离方程，有：

mgcosθ- N = ma1y     ③

对斜面，仍沿合加速度a2方向列方程，有：

Nsinθ= Ma2          ④

解①②③④式即可得a2 。

答案：a2 =  。

（学生活动）思考：如何求a1的值？

解：a1y已可以通过解上面的方程组求出；a1x只要看滑块的受力图，列x方向的隔离方程即可，显然有mgsinθ= ma1x ，得:a1x = gsinθ 。最后据a1 = 求a1 。

答：a1 =  。

2、如图21所示，与水平面成θ角的AB棒上有一滑套C ，可以无摩擦地在棒上滑动，开始时与棒的A端相距b ，相对棒静止。当棒保持倾角θ不变地沿水平面匀加速运动，加速度为a（且a＞gtgθ）时，求滑套C从棒的A端滑出所经历的时间。

解说：这是一个比较特殊的“连接体问题”，寻求运动学参量的关系似乎比动力学分析更加重要。动力学方面，只需要隔离滑套C就行了。

（学生活动）思考：为什么题意要求a＞gtgθ？（联系本讲第二节第1题之“思考题”）

定性绘出符合题意的运动过程图，如图22所示：S表示棒的位移，S1表示滑套的位移。沿棒与垂直棒建直角坐标后，S1x表示S1在x方向上的分量。不难看出：

S1x + b = S cosθ                   ①

设全程时间为t ，则有：

S = at2                          ②

S1x = a1xt2                        ③

而隔离滑套，受力图如图23所示，显然：

mgsinθ= ma1x                       ④

解①②③④式即可。

答案：t = 

另解：如果引进动力学在非惯性系中的修正式 Σ+ * = m （注：*为惯性力），此题极简单。过程如下——

以棒为参照，隔离滑套，分析受力，如图24所示。

注意，滑套相对棒的加速度a相是沿棒向上的，故动力学方程为：

F*cosθ- mgsinθ= ma相            （1）

其中F* = ma                      （2）

而且，以棒为参照，滑套的相对位移S相就是b ，即：

b = S相 = a相 t2                 （3）

解（1）（2）（3）式就可以了。

第二讲 配套例题选讲

教材范本：龚霞玲主编《奥林匹克物理思维训练教材》，知识出版社，2002年8月第一版。

例题选讲针对“教材”第三章的部分例题和习题。
如图9所示，质量都为m的小球A、B用轻绳挂在天花板上的O点，用F=mg的作用于球B上，且力F的方向始终垂直于AB，求最终系统平衡时OA段绳上拉力的大小.


违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网