题目内容
16.静水中的两只船静止在一条直线上,质量都是M(不包括人),甲船上质量为m的人跳到乙船上,又马上跳回甲船上,问甲,乙两船的速度之比是$\frac{M}{M+m}$.分析 人与两船组成的系统动量守恒,应用动量守恒定律,求出甲以两船的速度大小之比.
解答 解:人与甲乙两船组成的系统动量守恒,规定向甲船的速度方向为正方向,由动量守恒定律得:
(M+m)v甲-Mv乙=0,
解得:$\frac{{v}_{甲}}{{v}_{乙}}$=$\frac{M}{M+m}$;
故答案为:$\frac{M}{M+m}$.
点评 本题考查动量守恒定律的应用,运用动量守恒定律解题关键选择好系统,确定系统动量是否守恒,然后列式求解.

练习册系列答案
相关题目
6.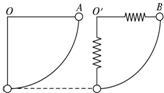 如图A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳和轻弹簧均处于水平,弹簧处于自然状态,将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上,则( )
如图A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳和轻弹簧均处于水平,弹簧处于自然状态,将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上,则( )
 如图A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳和轻弹簧均处于水平,弹簧处于自然状态,将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上,则( )
如图A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳和轻弹簧均处于水平,弹簧处于自然状态,将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上,则( )| A. | 两球到达各自悬点的正下方时,两球动能相等 | |
| B. | 两球到达各自悬点的正下方时,A球动能较大 | |
| C. | 两球到达各自悬点的正下方时,B球动能较大 | |
| D. | 两球到达各自悬点的正下方时,A球受到向上的拉力较小 |
4.从高处沿水平方向抛出一个物体,经时间t,该物体的瞬时速度的大小为vt,方向与水平方向夹角α,若不计空气阻力,则( )
| A. | 物体平抛的初速度为vtcosα | |
| B. | 物体平抛的初速度为gt•cotα | |
| C. | 物体在竖直方向的位移为$\frac{1}{2}$gt2sin2α | |
| D. | 物体在竖直方向的位移为$\frac{1}{2g}$vt2sin2α |
11.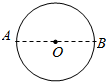 如图所示,一个人沿着一个圆形轨道运动,由A点开始运动,经过半个圆周到达B点,下列说法正确的是( )
如图所示,一个人沿着一个圆形轨道运动,由A点开始运动,经过半个圆周到达B点,下列说法正确的是( )
 如图所示,一个人沿着一个圆形轨道运动,由A点开始运动,经过半个圆周到达B点,下列说法正确的是( )
如图所示,一个人沿着一个圆形轨道运动,由A点开始运动,经过半个圆周到达B点,下列说法正确的是( )| A. | 人从A到B的平均速度方向由A指向B | |
| B. | 人从A到B的平均速度方向沿B点的切线方向 | |
| C. | 人在B点的瞬时速度方向由A指向B | |
| D. | 人在B点的瞬时速度方向沿B点的切线方向 |
9.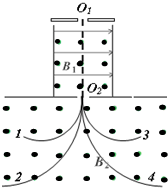 阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )
阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )
 阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )
阿尔法磁谱仪主要用于探索宇宙中的反物质,反物质是由反粒子组成的.带电粒子和它的反粒子质量相等,带电量相等但电性相反,例如反质子即为${\;}_{-1}^{1}$H.假若使一束质子、反质子、α粒子和反α粒子${\;}_{-2}^{4}$He组成的射线,沿直线O1O2进入匀强磁场B2而形成图示中的4条径迹则( )| A. | 径迹2的粒子比径迹1的粒子速度大 | |
| B. | 径迹4的粒子与径迹3的粒子在磁场中回旋时间相等 | |
| C. | 3是反α粒子径迹 | |
| D. | 4是反α粒子径迹 |
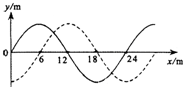 如图所示,实线是沿x轴传播的一列机械波在t=0时刻的波形图,虚线是这列波在t=1.5s时刻的波形图.已知波速是12m/s,则这列波的周期是2s,此波的传播方向为x轴的负方向传播(填:正或负).
如图所示,实线是沿x轴传播的一列机械波在t=0时刻的波形图,虚线是这列波在t=1.5s时刻的波形图.已知波速是12m/s,则这列波的周期是2s,此波的传播方向为x轴的负方向传播(填:正或负). 如图所示,竖直平面内有两个有界区域Ⅰ和Ⅱ,宽度均为L,竖直虚线是它们的分界线.区域Ⅰ中有垂直纸面向里的匀强磁场,区域Ⅱ中有匀强电场.质量为m、电量为q的带正电的粒子(重力不计)以初速度V0从O点沿水平方向射入磁场,运动到P点(图中未标出)离开磁场并进入电场,离开时速度方向与竖直方向成45°角,粒子经一段时间后到达电场右边界时速度恰好为零,此后再次从P点返问磁场.求:
如图所示,竖直平面内有两个有界区域Ⅰ和Ⅱ,宽度均为L,竖直虚线是它们的分界线.区域Ⅰ中有垂直纸面向里的匀强磁场,区域Ⅱ中有匀强电场.质量为m、电量为q的带正电的粒子(重力不计)以初速度V0从O点沿水平方向射入磁场,运动到P点(图中未标出)离开磁场并进入电场,离开时速度方向与竖直方向成45°角,粒子经一段时间后到达电场右边界时速度恰好为零,此后再次从P点返问磁场.求: