题目内容
7.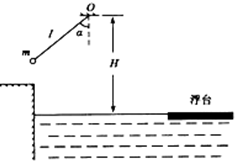 在游乐节目中,选手需要借助悬挂在高处的绳飞越到水面的浮台上,绳的悬挂点O距水面的高度为H=3m,绳的长度为l,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角为α,摆到最低点时的速率v=$\sqrt{gl}$.不计空气阻力和绳的质量,浮台露出水面的高度不计,取g=10m/s2.
在游乐节目中,选手需要借助悬挂在高处的绳飞越到水面的浮台上,绳的悬挂点O距水面的高度为H=3m,绳的长度为l,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角为α,摆到最低点时的速率v=$\sqrt{gl}$.不计空气阻力和绳的质量,浮台露出水面的高度不计,取g=10m/s2.(1)求选手摆到最低点时对绳的拉力大小;
(2)若选手摆到最低点时松手,小明认为绳越长,在浮台上的落点距岸边越远;小阳认为绳越短,落点距岸边越远,请通过推算说明你的观点.
分析 (1)在最低点,重力和拉力的合力提供向心力;用牛顿运动定律结合圆周运动的向心力求出绳子对选手的拉力;最后用牛顿第三定律求出选手对绳子的拉力.
(2)对平抛运动沿水平和竖直两个方向进行分解,水平方向上是匀速直线运动,竖直方向上时自由落体运动,分别列出位移式子,联立后进行数学分析,得出当l=1.5m时,水平方向具有最大值.
解答 解:(1)在最低点,重力和拉力的合力提供向心力,故:
F-mg=m$\frac{{v}^{2}}{l}$
其中:v=$\sqrt{gl}$
联立解得:
F=2mg=1200N
(2)对平抛运动,根据分位移公式,有:
H-l=$\frac{1}{2}g{t}^{2}$
x=vt
联立解得:
x=$\sqrt{2l(H-l)}$
根据公式a2+b2≥2ab,可知:
$2\sqrt{l}\sqrt{H-l}≤l+(H-l)=H$,当$\sqrt{l}=\sqrt{H-l}$,即l=1.5m时取“=”;
答:(1)选手摆到最低点时对绳的拉力大小为1200N;
(2)当l=1.5m时选手摆到最低点松手,运动到浮台处离岸水平距离最大.因此,两人的看法均不正确.当绳长钺接近1.5m时,落点距岸边越远.
点评 本题考查到了圆周运动向心力、平抛运动规律及求极值问题.解答第一问时,一定注意要求的是选手对绳子的拉力.解题过程中是对选手进行受力分析的,故不要忘记应用牛顿第三定律.关于物理当中的极值问题,要会熟练的对式子进行数学分析,从而得出结论.

练习册系列答案
相关题目
12.小明站在电梯里,当电梯以加速度5m/s2上升时,小明受到的支持力( )
| A. | 小于重力,但不为零 | B. | 大于重力 | ||
| C. | 等于重力 | D. | 等于零 |
18.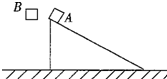 (多选)如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则(不计一切阻力)( )
(多选)如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则(不计一切阻力)( )
 (多选)如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则(不计一切阻力)( )
(多选)如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则(不计一切阻力)( )| A. | 下落过程,重力对两物体做的功相同 | |
| B. | 下落过程,重力的平均功率相同 | |
| C. | 到达底端时重力的瞬时功率PA<PB | |
| D. | 到达底端时两物体的速度相同 |
15.一定质量的理想气体,经图所示方向发生状态变化,在此过程中,下列叙述正确的是( )


| A. | 1→2气体体积增大 | B. | 3→1气体体积增大 | ||
| C. | 2→3气体体积不变 | D. | 3→1→2气体体积不断减小 |
2.一定质量的理想气体由状态A经过如图所示过程变到状态B,在此过程中气体的密度( )
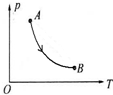

| A. | 一直变大 | B. | 先变小后变大 | C. | 一直变小 | D. | 先变大后变小 |
12.某一物体在质量不变的情况下,下列说法中正确的是( )
| A. | 物体动量改变,其速度大小一定改变 | |
| B. | 物体的速度方向改变,其动量不一定改变 | |
| C. | 物体的运动状态改变,其动量可能不变 | |
| D. | 物体的动能不变,其动量可能改变 |
19.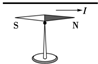 如图所示,把一条导线平行地放在磁针的上方附近,当导线中有电流通过时,磁针会发生偏转.发现这个实验现象的物理学家是( )
如图所示,把一条导线平行地放在磁针的上方附近,当导线中有电流通过时,磁针会发生偏转.发现这个实验现象的物理学家是( )
 如图所示,把一条导线平行地放在磁针的上方附近,当导线中有电流通过时,磁针会发生偏转.发现这个实验现象的物理学家是( )
如图所示,把一条导线平行地放在磁针的上方附近,当导线中有电流通过时,磁针会发生偏转.发现这个实验现象的物理学家是( )| A. |  牛顿 | B. |  爱因斯坦 | C. |  奥斯特 | D. |  居里夫人 |
16.贫铀炸弹是一种杀伤力很强的武器,贫铀是提炼铀235以后的副产品,其主要成分为铀238,贫铀炸弹不仅有很强的穿甲能力,而且铀238具有放射性,会发生α衰变.残留物可长期对环境起破坏作用而造成污染.人长期生活在该环境中会受到核辐射而患上皮肤癌和白血病.下列说法正确的是 ( )
| A. | 铀238的衰变方程式为:${\;}_{92}^{238}U$+${\;}_0^1n$→${\;}_{90}^{234}Th$+${\;}_2^4He$ | |
| B. | ${\;}_{92}^{235}U$和${\;}_{92}^{238}U$互为同位素 | |
| C. | 人患皮肤癌和白血病是因为核辐射导致了基因突变 | |
| D. | 贫铀弹的穿甲能力很强,也是因为它的放射性 | |
| E. | 铀238的衰变方程式为:${\;}_{92}^{238}U$→${\;}_{90}^{234}Th$+${\;}_{2}^{4}$He |
17.如图所示是A、B两质点从同一地点运动的x-t图象,则下列说法中正确的是( )
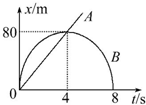

| A. | A质点以20m/s的速度匀速运动 | |
| B. | B质点先沿正方向做直线运动,后沿负方向做直线运动 | |
| C. | B质点最初4s做加速运动,后4s做减速运动 | |
| D. | A、B两质点在4s末相遇 |