题目内容
 (2010?南开区一模)如图所示,坐标系xOy在竖直平面内,空间有沿水平方向垂直于纸面向外的匀强磁场,磁感应强度大小为B,在x>0的空间里有沿x轴正方向的匀强电场,场强的大小为E,一个带正电的小球经过图中的x轴上的A点,沿着与水平方向成θ=30°角的斜向下直线做匀速运动,经过y轴上的B点进入x<0的区域,要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域另加一匀强电场,若带电小球做圆周运动通过x轴上的C点(C点未标出),且
(2010?南开区一模)如图所示,坐标系xOy在竖直平面内,空间有沿水平方向垂直于纸面向外的匀强磁场,磁感应强度大小为B,在x>0的空间里有沿x轴正方向的匀强电场,场强的大小为E,一个带正电的小球经过图中的x轴上的A点,沿着与水平方向成θ=30°角的斜向下直线做匀速运动,经过y轴上的B点进入x<0的区域,要使小球进入x<0区域后能在竖直面内做匀速圆周运动,需在x<0区域另加一匀强电场,若带电小球做圆周运动通过x轴上的C点(C点未标出),且. |
| OA |
. |
| OC |
(1)小球运动速率的大小;
(2)在x<0的区域所加电场的场强大小和方向;
(3)小球从B点运动到C点所用时间.
分析:(1)球在AB段做匀速直线运动,重力、电场力和洛伦兹力三力平衡,由平衡条件可求解小球运动的速度大小;
(2)小球进入x<0区域后在竖直面内做匀速圆周运动,则电场力与重力平衡,即可求得场强大小和方向;
(3)球在磁场中做匀速圆周运动的周期是T=
,画出小球运动轨迹,确定出轨迹对应的圆心角,可求出时间.
(2)小球进入x<0区域后在竖直面内做匀速圆周运动,则电场力与重力平衡,即可求得场强大小和方向;
(3)球在磁场中做匀速圆周运动的周期是T=
| 2πR |
| v |
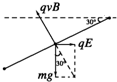
解答:解:(1)小球从A运动到B的过程中,小球受重力、电场力和洛伦兹力作用而处于平衡状态,如图右图所示.由题设条件知sin30°=
,
所以小球的运动速率为 v=
.
(2)小球在x<0的区域做匀速圆周运动,则小球的重力与所受的电场力平衡,洛伦兹力提供做圆周运动的向心力.则
mg=qE,
又 tan30°=
.
所以 E′=
E,方向竖直向上.
(3)如图所示,连接BC,过B作AB的垂线交x轴于O′.
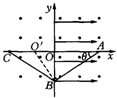 因为 θ=30°,所以∠AO′B=60°,又
因为 θ=30°,所以∠AO′B=60°,又
=
,
故∠OCB=θ=30°,所以∠CBO′=30°,
=
,则O’为小球做圆周运动的圆心
且 qvB=m
,R=
,T=
=
,
由于∠CO′B=120°,
小球从点B运动到点C的时间为 t1=
T=
,
又
=
,所以
=
.t1=
答:
(1)小球运动速率的大小为
.
(2)在x<0的区域所加电场的场强大小为
E,方向竖直向上.
(3)小球从B点运动到C点所用时间是
.
| qE |
| Bqv |

所以小球的运动速率为 v=
| 2E |
| B |
(2)小球在x<0的区域做匀速圆周运动,则小球的重力与所受的电场力平衡,洛伦兹力提供做圆周运动的向心力.则
mg=qE,
又 tan30°=
| qE |
| mg |
所以 E′=
| 3 |
(3)如图所示,连接BC,过B作AB的垂线交x轴于O′.
 因为 θ=30°,所以∠AO′B=60°,又
因为 θ=30°,所以∠AO′B=60°,又. |
| OA |
. |
| OC |
故∠OCB=θ=30°,所以∠CBO′=30°,
. |
| O′C |
. |
| O′B |
且 qvB=m
| v2 |
| R |
| mv |
| Bq |
| 2πR |
| v |
| 2πm |
| Bq |
由于∠CO′B=120°,
小球从点B运动到点C的时间为 t1=
| 1 |
| 3 |
| 2πm |
| 3Bq |
又
| m |
| q |
| ||
| g |
. |
| OA |
3
| ||
| gB2 |
2
| ||
| 3gB |
答:
(1)小球运动速率的大小为
| 2E |
| B |
(2)在x<0的区域所加电场的场强大小为
| 3 |
(3)小球从B点运动到C点所用时间是
2
| ||
| 3gB |
点评:本题是带电体在复合场中运动的类型,分析受力情况和运动情况是基础,小球做匀速圆周运动时,画出轨迹,由几何知识确定圆心角是求解运动时间的关键.

练习册系列答案
相关题目
 (2010?南开区一模)如图所示,一个理想变压器,原、副线圈匝数之比为n1:n2=10:1,在原线圈ab两端加上电压为u=311sin100πt V的正弦交流电,当原线圈中电流瞬时值为零时,副线圈c、d两端电压的瞬时值为( )
(2010?南开区一模)如图所示,一个理想变压器,原、副线圈匝数之比为n1:n2=10:1,在原线圈ab两端加上电压为u=311sin100πt V的正弦交流电,当原线圈中电流瞬时值为零时,副线圈c、d两端电压的瞬时值为( )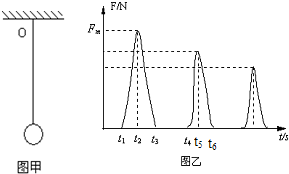 (2010?南开区一模)利用传感器和计算机可以研究快速变化力的大小,实验时,把图甲中的小球举高到绳子的悬点O处,然后让小球自由下落.用这种方法获得的弹性绳的拉力随时间变化图线如图乙所示.根据图线所提供的信息,以下判断正确的是( )
(2010?南开区一模)利用传感器和计算机可以研究快速变化力的大小,实验时,把图甲中的小球举高到绳子的悬点O处,然后让小球自由下落.用这种方法获得的弹性绳的拉力随时间变化图线如图乙所示.根据图线所提供的信息,以下判断正确的是( ) (2010?南开区一模)如图所示,三条平行等距的虚线表示电场中的三个等势面,电势值分别为10V、20V、30V,实线是一带负电的粒子(不计重力)在该区域内的运动轨迹,对于轨迹上的a、b、c三点来说( )
(2010?南开区一模)如图所示,三条平行等距的虚线表示电场中的三个等势面,电势值分别为10V、20V、30V,实线是一带负电的粒子(不计重力)在该区域内的运动轨迹,对于轨迹上的a、b、c三点来说( )