题目内容
20.汽车A以vA=4m/s的速度向右做匀速直线运动,发现前方相距x0=7m处,以vB=10m/s的速度同向运动的B汽车正开始以大小为a=2m/s2的加速度刹车,从此刻开始计时,求:(1)A追上B前,A、B间的最远距离是多少?
(2)经过多长时间A恰好追上B?
分析 (1)当两车速度相等时,相距最远,结合速度时间公式求出速度相等的时间,根据位移公式,结合位移关系求出最远距离.
(2)根据位移关系,结合运动学公式求出追及的时间.
解答 解:(1)两车速度相等经历的时间${t}_{1}=\frac{{v}_{B}-{v}_{A}}{a}=\frac{10-4}{2}s=3s$,
则A、B的最远距离$△x=\frac{{{v}_{B}}^{2}-{{v}_{A}}^{2}}{2a}+{x}_{0}-{v}_{A}{t}_{1}$=$\frac{100-16}{4}+7-4×3$m=16m.
(2)B速度减为零的时间${t}_{2}=\frac{{v}_{B}}{a}=\frac{10}{2}s=5s$,减为零的位移${x}_{B}=\frac{{{v}_{B}}^{2}}{2a}=\frac{100}{4}m=25m$.
此时A的位移xA=vAt2=4×5m=20m,
因为xA<xB+7m,可知B速度减为零时,A还未追上B.
还需追及的时间${t}_{3}=\frac{{x}_{B}+7-{x}_{A}}{{v}_{A}}=\frac{25+7-20}{4}s=3s$,
则t=t2+t3=5+3s=8s.
答:(1)A追上B前,A、B间的最远距离是16m.
(2)经过8s时间A恰好追上B.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时,两车具有最大距离.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
10.如图所示,在水平桌面上叠放着木块A、B和C,水平力F推动三个木块匀速运动,下列说法正确的是( )


| A. | B受4个力C受4个力 | B. | B受5个力C受4个力 | ||
| C. | B受5个力C受5个力 | D. | B受6个力C受5个力 |
11.一物体自t=0时开始做直线运动,其速度图线如图所示.下列选项正确的是( )


| A. | 在0~6s内,物体离出发点的最远距离为30m | |
| B. | 在0~6s内,物体经过的路程为40m | |
| C. | 在0~4s内,物体的平均速率为5m/s | |
| D. | 在5~6s 内,物体所受的合外力做负功 |
8.下述关于用多用表欧姆档测电阻的说法中正确的是( )
| A. | 测量电阻时如果指针偏转过大,应将选择开关S拨至倍率较小的档位 | |
| B. | 测量定值电阻时,如果红、黑表笔分别插在负、正插孔,不会影响测量结果 | |
| C. | 测量电路中的某个电阻,应该把该电阻与电路断开 | |
| D. | 测量阻值不同的电阻时都必须重新调零 |
15. 酒精测试仪用于机动车驾驶人员是否酗酒及其他严禁酒后作业人员的现场检测.它是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,不同的酒精气体浓度对应着传感器的不同电阻,这样,电压表的指针就与酒精气体浓度有了对应关系.如果二氧化锡半导体型酒精气体传感器电阻的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
酒精测试仪用于机动车驾驶人员是否酗酒及其他严禁酒后作业人员的现场检测.它是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,不同的酒精气体浓度对应着传感器的不同电阻,这样,电压表的指针就与酒精气体浓度有了对应关系.如果二氧化锡半导体型酒精气体传感器电阻的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
 酒精测试仪用于机动车驾驶人员是否酗酒及其他严禁酒后作业人员的现场检测.它是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,不同的酒精气体浓度对应着传感器的不同电阻,这样,电压表的指针就与酒精气体浓度有了对应关系.如果二氧化锡半导体型酒精气体传感器电阻的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )
酒精测试仪用于机动车驾驶人员是否酗酒及其他严禁酒后作业人员的现场检测.它是一种二氧化锡半导体型酒精气体传感器,酒精气体传感器的电阻随酒精气体浓度的变化而变化,在如图所示的电路中,不同的酒精气体浓度对应着传感器的不同电阻,这样,电压表的指针就与酒精气体浓度有了对应关系.如果二氧化锡半导体型酒精气体传感器电阻的倒数与酒精气体的浓度成正比,那么,电压表示数U与酒精气体浓度c之间的对应关系正确的是( )| A. | U越大,表示c越大,c与U成正比 | |
| B. | U越大,表示c越大,但是c与U不成正比 | |
| C. | U越大,表示c越小,c与U成反比 | |
| D. | U越大,表示c越小,但是c与U不成反比 |
12.下图中描述质点做匀速直线运动的是( )
| A. | 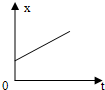 | B. | 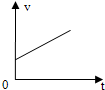 | C. | 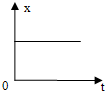 | D. | 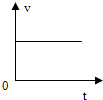 |
5.一物体只受到F1、F2、F3三个力作用,做匀速直线运动,这三个力的大小不可能是( )
| A. | 1N,3N,5N | B. | 2N,4N,6N | C. | 3N,5N,7N | D. | 4N,6N,8N |
 如图是用打点计时器测定匀变速直线运动的加速度时得到的纸带,从O点开始每5个点一个计数点,则每两个计数点的时间间隔为0.1s,测得OA=6.80cm,CD=3.20cm,DE=2.00cm,则物体运动加速度为-1.2m/s2,D点的速度为0.26m/s.
如图是用打点计时器测定匀变速直线运动的加速度时得到的纸带,从O点开始每5个点一个计数点,则每两个计数点的时间间隔为0.1s,测得OA=6.80cm,CD=3.20cm,DE=2.00cm,则物体运动加速度为-1.2m/s2,D点的速度为0.26m/s.