题目内容
6.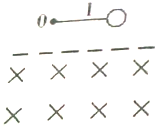 一半径为r、质量为m、电阻为R的金属圆环,用一长为l的绝缘细线悬挂于O点,在O点下方的$\frac{l}{2}$处有水平方向的匀强磁场,如图所示,拿着金属环使悬线水平,然后由静止释放,求:
一半径为r、质量为m、电阻为R的金属圆环,用一长为l的绝缘细线悬挂于O点,在O点下方的$\frac{l}{2}$处有水平方向的匀强磁场,如图所示,拿着金属环使悬线水平,然后由静止释放,求:(1)金属环要进入磁场时的速度大小;
(2)金属环在整个运动过程中产生的焦耳热.
分析 (1)根据机械能守恒定律,即可求解环要进入磁场时的速度大小;
(2)根据感应电流产生条件,只有环进入或离开磁场时,才会产生焦耳热,当环只能在磁场中运动时,即不会产生焦耳热,从而动能的减小,即为产生焦耳热.
解答 解:(1)根据机械能守恒,则有:$\frac{1}{2}m{v}^{2}=mg\frac{l}{2}$;
解得:v=$\sqrt{gl}$
(2)环在进或出磁场时,因切割磁感线,从而产生焦耳热;
从环以mg$\frac{l}{2}$的动能进入磁场后,来回进或出磁场,产生焦耳热,当环在刚进入磁场或刚出磁场速度为零时,环不会离开磁场,因此也不会产生焦耳热;
由能量守恒定律,则有:在整个运动过程中产生的焦耳热Q,即为减小的动能;
因此Q=mg$\frac{l}{2}$
答:(1)金属环要进入磁场时的速度大小$\sqrt{gl}$;
(2)金属环在整个运动过程中产生的焦耳热mg$\frac{l}{2}$.
点评 考查机械能守恒定律的应用,注意其守恒的条件,掌握焦耳热的产生的条件,理解能量守恒定律的应用.注意环不再出磁场时,就没有焦耳热产生是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
17. 如图所示,在斜向上的恒力F作用下,质量都为m的A、B两小斜面体保持相对静止一起沿竖直墙面向下做匀加速直线运动,恒力F与竖直方向的夹角为β,A、B接触面与水平方向的夹角为α.A与墙面间动摩擦因数为μ1,A与B间动摩擦因数为μ2.关于小斜面体A的受力情况,下列说法中正确的是( )
如图所示,在斜向上的恒力F作用下,质量都为m的A、B两小斜面体保持相对静止一起沿竖直墙面向下做匀加速直线运动,恒力F与竖直方向的夹角为β,A、B接触面与水平方向的夹角为α.A与墙面间动摩擦因数为μ1,A与B间动摩擦因数为μ2.关于小斜面体A的受力情况,下列说法中正确的是( )
 如图所示,在斜向上的恒力F作用下,质量都为m的A、B两小斜面体保持相对静止一起沿竖直墙面向下做匀加速直线运动,恒力F与竖直方向的夹角为β,A、B接触面与水平方向的夹角为α.A与墙面间动摩擦因数为μ1,A与B间动摩擦因数为μ2.关于小斜面体A的受力情况,下列说法中正确的是( )
如图所示,在斜向上的恒力F作用下,质量都为m的A、B两小斜面体保持相对静止一起沿竖直墙面向下做匀加速直线运动,恒力F与竖直方向的夹角为β,A、B接触面与水平方向的夹角为α.A与墙面间动摩擦因数为μ1,A与B间动摩擦因数为μ2.关于小斜面体A的受力情况,下列说法中正确的是( )| A. | 若μ1=μ2=0,小斜面体A只受2个力作用 | |
| B. | 若μ1=μ2=0,小斜面体A只受3个力作用 | |
| C. | 若μ1=0,μ2≠0,小斜面体B一定对A有摩擦力 | |
| D. | 若μ1≠0,μ2≠0,小斜面体B对A可能没有摩擦力 |
1.奥斯特、法拉第、安培、楞次等人对电磁学的发展起到了重要的作用,以下关于他们的贡献描述符合事实的是( )
| A. | 奥斯特首先发现电流的磁效应 | |
| B. | 安培首先提出了电场和电场线的概念 | |
| C. | 楞次总结出了感应电流方向所应满足的规律 | |
| D. | 法拉第总结出了影响感应电动势大小的因素. |
11.如图所示,下列有关电磁现象中说法不正确的是( )


| A. | 在图(1)情境中一固定的闭合线圈能使震动的磁铁较快地停下来 | |
| B. | 在图(2)小永磁铁从竖直放置的无裂缝甲铝管中下落与有裂缝乙铝管中下落的情况一致 | |
| C. | 在图(3)情境中磁铁能使绕自由转动的铜盘较快地停下来 | |
| D. | 在图(4)中放置于水平绝缘桌面的金属圆环将受到和磁铁运动方向相同的驱动力 |
15.关于离心运动,下列说法中正确的是( )
| A. | 物体突然受到向心力的作用,将做离心运动 | |
| B. | 做匀速圆周运动的物体,在外界提供的向心力突然变大时将做离心运动 | |
| C. | 做匀速圆周运动的物体,只要向心力的数值发生变化,就将做离心运动 | |
| D. | 做匀速圆周运动的物体,当外界提供的向心力突然消失或变小时将做离心运动 |
16. 如图所示,假定从某一星球(星球半径为R0)上在B点以速度v=9km/s发射一艘飞船,飞船在无动力飞行时其飞行轨道为如图所示的椭圆轨道.最远点A离星球表面高2R0,其周期为T.若该星球表面附近的重力加速度为g0,(忽略星球自转,同时不考虑大气的影响)则( )
如图所示,假定从某一星球(星球半径为R0)上在B点以速度v=9km/s发射一艘飞船,飞船在无动力飞行时其飞行轨道为如图所示的椭圆轨道.最远点A离星球表面高2R0,其周期为T.若该星球表面附近的重力加速度为g0,(忽略星球自转,同时不考虑大气的影响)则( )
 如图所示,假定从某一星球(星球半径为R0)上在B点以速度v=9km/s发射一艘飞船,飞船在无动力飞行时其飞行轨道为如图所示的椭圆轨道.最远点A离星球表面高2R0,其周期为T.若该星球表面附近的重力加速度为g0,(忽略星球自转,同时不考虑大气的影响)则( )
如图所示,假定从某一星球(星球半径为R0)上在B点以速度v=9km/s发射一艘飞船,飞船在无动力飞行时其飞行轨道为如图所示的椭圆轨道.最远点A离星球表面高2R0,其周期为T.若该星球表面附近的重力加速度为g0,(忽略星球自转,同时不考虑大气的影响)则( )| A. | 飞船在最远点A的速度为3km/s | |
| B. | 飞船在最远点A的加速度为$\frac{{g}_{0}}{4}$ | |
| C. | 若飞船在椭圆轨道上的A点要变轨到图示的大圆轨道,应该加速,加速后如能刚好做半径为3R0的圆周运动,则周期较椭圆轨道时长 | |
| D. | 若飞船在沿大圆轨道飞行时在A点一个零件脱落,则这个零件将做自由落体运动 |
 一质量为1kg的物体在恒力F作用下从水平地面上的A点由静止开始向C点运动,其中AB段光滑,BC段粗糙,物体运动到B点后立即做匀速运动,已知AC间距为100m,物体由A点运动到C点共用11s,物体在AB段运动的第2s内通过的距离为7.5m.
一质量为1kg的物体在恒力F作用下从水平地面上的A点由静止开始向C点运动,其中AB段光滑,BC段粗糙,物体运动到B点后立即做匀速运动,已知AC间距为100m,物体由A点运动到C点共用11s,物体在AB段运动的第2s内通过的距离为7.5m.



