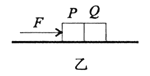
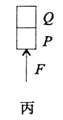
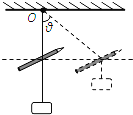
��Ŀ����
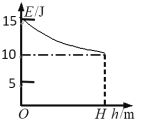
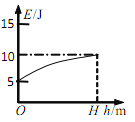
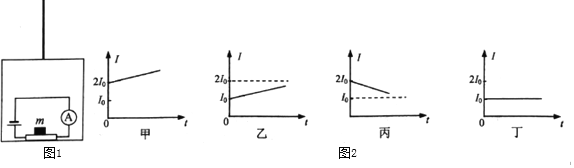
����Ŀ����ͼ����ʾ��MN��PQΪˮƽ���õ��㹻����ƽ�й⻬���죬������LΪ0.5m�������������һ����ֵΪ2���Ķ�ֵ����R����һ������Ϊ0.2kg�Ľ�����cd��ֱ�����ڵ����ϣ����뵼��Ӵ����ã�������cd�ĵ���r=2����������費�ƣ�����װ�ô��ڴ�ֱ����ƽ�����µ���ǿ�ų��У��Ÿ�Ӧǿ��B=2T��������1m/s�ij��ٶ������˶���ͬʱ��ʩ��ˮƽ���ҵ�����F���ã������������Ĺ��ʺ�Ϊ4W���Ӵ�ʱ��ʼ��ʱ������2s����������ٶȱ����ȶ����䣬ͼ��Ϊ��������ʱ��Ĺ�ϵͼ�����ʣ�
��1��������cd��ʼ�˶�ʱ���еĵ�������������
��2����������ǰ2s����������һ���������˶�����˵�����ɡ�
��3��2s����������ٶȴ�С�Ƕ���m/s��
��4��0��2s��ͨ������R�ĵ���Լ����C��
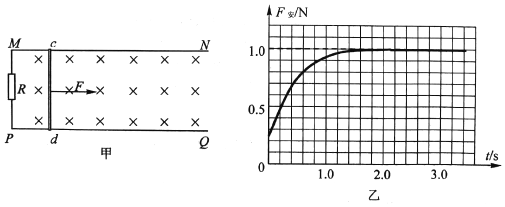
���𰸡�(1)dָ��c��(2)���ٶȼ�С�ļ���ֱ���˶���(3)4m/s��(4)1.66C
��������
��1�������ֶ����֪������cd�еĵ�������2������������������������ţ�ٵڶ������ж�������˶��������3�����������ٶ����ʱ�����ܵĺ�����Ϊ�㣬�Ӷ��������ٶȣ���4������ͼ��� ���������ⰲ�����ij�������ϵ����Ĺ�ʽ������.
��1�������ֶ����֪��������cd�еĵ���������dָ��c��
��2����������ǰ2s���������Ǽ��ٶȼ�С�ļ���ֱ���˶������ڽ������˶�����ʼʱ�̣���������ˮƽ�������ܵ�������FA������F�����ã�![]()
![]()
����F>FA�����������ܵĺ�����������ٶȷ�����ͬ����˽����������������˶�������![]() ������FA������v���������������������
������FA������v���������������������![]() ������F����v����������ϼ�С��
������F����v����������ϼ�С��
��F-FA=ma�����Լ��ٶ�a�����ϼ�С�����Խ�������ǰ2s����������һ�ּ��ٶȼ�С�ļ���ֱ���˶�.
��3�����������ٶ����ʱ�����ܵĺ�����Ϊ�㣬��![]()
�����![]()
��4��ͼ�������֮�乲Լ83��81-85����С������Ӧ�ġ������Ϊ![]()
��![]()
��![]() ��1.62C-1.70C��
��1.62C-1.70C��