题目内容
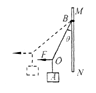
【题目】如图所示,在光滑的水平桌面上有一光滑小孔O,一根轻绳穿过小孔,一端连接质量为m=1kg的小球A,另一端与地面上质量为M=4kg的重物B连接。当OA距离R=0.1m时,绳子恰好拉直,(g=10m/s2)求:
(1)当A球以角速度ù=10rad/s,半径为R做匀速圆周运动时,B对地面的压力是多少?
(2) 要使B对地面恰好无压力,A球的角速度应为多大?
【答案】(1)30N,方向竖直向下;(2)20rad/s
【解析】
(1)对小球A来说,小球受到的重力和支持力平衡.因此绳子的拉力提供向心力,
则:FT=mRω2=1×0.1×102N=10N,
对物体B来说,物体受到三个力的作用:重力Mg、绳子的拉力FT、地面的支持力FN,
由力的平衡条件可得:FT+FN=Mg
故FN=Mg-FT
将FT=10N代入可得:FN=(4×10-10)N=30N
由牛顿第三定律可知,B对地面的压力为30N,方向竖直向下.
(2)当B对地面恰好无压力时,有:Mg=FT′,
拉力FT′提供小球A所需向心力,则:FT′=mRω′2
则有:![]()
即:当B对地面恰好无压力时,A小球的角速度值应为20rad/s.

练习册系列答案
相关题目