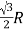题目内容
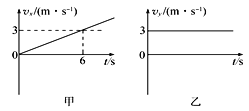
【题目】如图甲所示,质量M=4 kg且足够长的木板静止在光滑的水平面上,在木板的中点放一个质量m=4 kg大小可以忽略的铁块,铁块与木板之间的动摩擦因数μ=0.2,设最大静摩擦力等于滑动摩擦力.两物体开始均静止,从t=0时刻起铁块m受到水平向右、大小如图乙所示的拉力F的作用,F共作用时间为6 s,(g取10 m/s2)求:
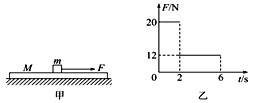
(1)铁块和木板在前2 s的加速度大小分别为多少?
(2)铁块在6s内的位移大小为多少?
(3)从开始运动到铁块和木板相对静止时它们的相对位移大小为多少?
【答案】(1)![]() (2)39m(3)4m
(2)39m(3)4m
【解析】
(1)前2 s,由牛顿第二定律得
对铁块:F-μmg=ma1,
解得a1=3 m/s2
对木板:μmg=Ma2,
解得a2=2 m/s2
(2) t1=2 s内,铁块的位移x1=![]() a1t12=6 m
a1t12=6 m
木板的位移 x2=![]() a2t12=4 m
a2t12=4 m
2 s末,铁块的速度v1=a1t1=6 m/s
木板的速度 v2=a2t1=4 m/s
2 s后,由牛顿第二定律,对铁块:F′-μmg=ma1′
解得a1′=1 m/s2
对木板:μmg=Ma2′,解得a2′=2 m/s2
设再经过t2时间铁块和木板的共同速度为v,则
v=v1+a1′t2=v2+a2′t2
解得t 2=2 s, v=8 m/s
在t2时间内,铁块的位移x1′=![]() t0=
t0=![]() ×2 m=14 m
×2 m=14 m
木板的位移 x2′=![]() t2=
t2=![]() ×2 m=12 m
×2 m=12 m
F作用的最后2 s,铁块和木板相对静止,一起以初速度v=8 m/s做匀加速直线运动,由牛顿第二定律,对铁块和木板整体有
F=(M+m)a,解得a=1.5 m/s2
最后2 s铁块和木板运动的位移均为
x3=vΔt+![]() a(Δt)2=19 m
a(Δt)2=19 m
所以铁块在6内的运动的总位移为
x铁块=x1+x1′+x3=39 m
(3)铁块和木板相对静止前木板运动的总位移x木板=x2+x2′=16 m
铁块和木板的相对位移大小 x1+x1′-x木板=4 m