题目内容
如图（a）所示，平行金属导轨MN、PQ光滑且足够长，固定在同一水平面上，两导轨间距L＝0．25 m，电阻R＝0．5 Ω，导轨上停放一质量m＝0．1 kg、电阻r＝0．1 Ω的金属杆，导轨电阻可忽略不计，整个装置处于磁感应强度B＝0．4 T的匀强磁场中，磁场方向竖直向下，现用一外力F沿水平方向拉杆，使其由静止开始运动，理想电压表的示数U随时间t变化的关系如图（b）所示．
（1）分析证明金属杆做匀加速直线运动；
（2）求金属杆运动的加速度；
（3）写出外力F随时间变化的表达式；
（4）求第2．5 s末外力F的瞬时功率．
（1）分析证明金属杆做匀加速直线运动；
（2）求金属杆运动的加速度；
（3）写出外力F随时间变化的表达式；
（4）求第2．5 s末外力F的瞬时功率．
（1）见解析 （2）2．4 m/s2 （3）F＝0．04t＋0．24 N （4）2．04 W
（1）U＝E·
＝
，U∝v，因U随时间均匀变化，故v也随时间均匀变化，金属杆做匀加速直线运动．
（2）由图象k＝
＝
·
＝a·则金属杆运动的加速度
a＝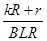
＝
m/s2＝2．4 m/s2．
（3）由牛顿第二定律F＝F安＋ma＝BIL＋ma＝
＋ma＝0．04t＋0．24（N）．
（4）第2．5 s末外力F的瞬时功率P＝Fv＝（0．04t＋0．24）at＝2．04 W．
答案：（1）见解析 （2）2．4 m/s2 （3）F＝0．04t＋0．24 N （4）2．04 W
本题考查法拉第电磁感应定律和电路的结合问题，根据导体棒切割磁感线，以及Ut图像判断导体棒做匀加速直线运动，由楞次定律求出加速度a
＝，U∝v，因U随时间均匀变化，故v也随时间均匀变化，金属杆做匀加速直线运动．（2）由图象k＝
＝·＝a·则金属杆运动的加速度a＝
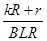＝ m/s2＝2．4 m/s2．（3）由牛顿第二定律F＝F安＋ma＝BIL＋ma＝
＋ma＝0．04t＋0．24（N）．（4）第2．5 s末外力F的瞬时功率P＝Fv＝（0．04t＋0．24）at＝2．04 W．
答案：（1）见解析 （2）2．4 m/s2 （3）F＝0．04t＋0．24 N （4）2．04 W
本题考查法拉第电磁感应定律和电路的结合问题，根据导体棒切割磁感线，以及Ut图像判断导体棒做匀加速直线运动，由楞次定律求出加速度a
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
，在其上放置一矩形金属线框
，
的边长
，
的边长
，线框的质量
，电阻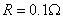
，线框通过细线绕过定滑轮与重物相连，细线与斜面平行且靠近。重物质量
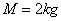，离地面的高度为
。斜面上
区域是有界匀强磁场，方向垂直于斜面向上，已知AB到
的距离为
，
的距离为
，
，取
。现让线框从静止开始运动（开始时刻
与AB边重合），发现线框匀速穿过匀强磁场区域，求：
图象
