题目内容
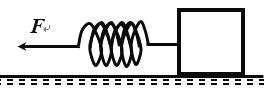
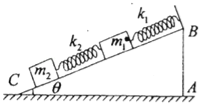
【题目】如图所示，倾角为θ的光滑斜面ABC放在水平面上，劲度系数分别为k1、k2的两个轻弹簧沿斜面悬挂着，两弹簧之间有一质量为m1的重物，最下端挂一质量为m2的重物，此时两重物处于平衡状态，现把斜面ABC绕A点缓慢地顺时针旋转90°后，重新达到平衡．试求：m1、m2沿斜面各移动的距离．
【答案】m1、m2沿斜面移动的距离各为
和
（sinθ+cosθ）+
（sinθ+cosθ）．
【解析】
试题在旋转前后，物体均处于平衡状态，则共点力的平衡条件可得出物体弹簧弹力，由胡克定律可求得弹簧的伸长量，则可得出旋转前后的距离．
解：没旋转时，两弹簧均处于伸长状态，两弹簧伸长量分别为x1、x2，
由平衡条件可知k2x2=m2gsinθ，解得：x2=
k2x2+m1gsinθ=k1x1
解得：x1=
旋转后，两弹簧均处于压缩状态，压缩量为x1′，x2′
m2gcosθ=k2x2′
解得：x2′=
（m1+m2）gcosθ=k1x1′
解得：x1′=
所以m1移动的距离d1=x1+x1′=
m2移动的距离d2=x2+x2′+d1=
（sinθ+cosθ）+（sinθ+cosθ）
答：m1、m2沿斜面移动的距离各为和（sinθ+cosθ）+（sinθ+cosθ）．
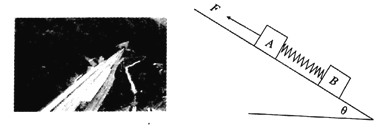
100分闯关期末冲刺系列答案
【题目】现用频闪照相方法来研究物块的变速运动．在一小物块沿斜面向下运动的过程中，用频闪相机拍摄的不同时刻物块的位置如图所示．拍摄时频闪频率是10Hz；通过斜面上固定的刻度尺读取的5个连续影像间的距离依次为x1、x2、x3、x4．已知斜面顶端的高度h和斜面的长度s．数据如下表所示．重力加速度大小g=9.80m/s2．
单位：cm
x1 | x2 | x3 | x4 | h | S |
10.76 | 15.05 | 19.34 | 23.65 | 48.00 | 80.00 |
根据表中数据，完成下列填空：
（1）物块的加速度a=_____m/s2（保留3位有效数字）．
（2）因为_____可知斜面是粗糙的．
