题目内容
6.如图1,MN、PQ两条平行的光滑金属轨道与水平面成θ=30°角固定,轨距为L=1m,质量为m的金属杆ab水平放置在轨道上,其阻值忽略不计.空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B=0.5T.P、M间接有阻值R1的定值电阻,Q、N间接变阻箱R.现从静止释放ab,改变变阻箱的阻值R,测得最大速度为vm,得到$\frac{1}{Vm}$与$\frac{1}{R}$的关系如图2所示.若轨道足够长且电阻不计,重力加速度g取l0m/s2.求:(1)金属杆的质量m和定值电阻的阻值R1;
(2)当变阻箱R取1Ω时,且金属杆ab运动的加速度为0.5gsinθ时,此时金属杆ab运动的速度;
(3)当变阻箱R取1Ω时,且金属杆ab运动的速度为$\frac{Vm}{2}$时,定值电阻R1消耗的电功率.
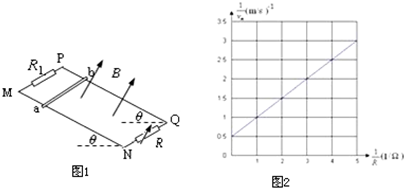
分析 (1)从静止释放ab,ab棒切割磁感线产生感应电动势,相当于电源,定值电阻R1与R并联,可求得总电阻的表达式.当ab棒匀速运动时,速度达到最大,根据平衡条件和安培力公式到$\frac{1}{{v}_{m}}$与$\frac{1}{R}$的关系式,由图象读出斜率造型截距,即可求出m和R1.
(2)当变阻箱R取1Ω时,且金属杆ab运动的加速度为$\frac{1}{2}$gsinθ时,根据牛顿第二定律求得此时金属杆ab运动的速度;
(3)当变阻箱R取1Ω时,由图象得到vm,由公式P=$\frac{{E}^{2}}{{R}_{1}}$求得定值电阻R1消耗的电功率.
解答 解:(1)总电阻为R总=$\frac{{R}_{1}R}{{R}_{1}+R}$;
通过金属杆ab的电流为I=$\frac{BLv}{{R}_{总}}$
当达到最大速度时金属棒受力平衡,则有mgsinθ=BIL=$\frac{{B}^{2}{L}^{2}{v}_{m}}{{R}_{1}R}({R}_{1}+R)$
得,$\frac{1}{{v}_{m}}$=$\frac{{B}^{2}{L}^{2}}{mgRsinθ}$+$\frac{{B}^{2}{L}^{2}}{mg{R}_{1}sinθ}$
根据图象得到斜率k=0.5,纵截距b=0.5,
由数学知识得:k=$\frac{{B}^{2}{L}^{2}}{mgsinθ}$,b=$\frac{{B}^{2}{L}^{2}}{mg{R}_{1}sinθ}$
代入数据,可以得到棒的质量m=0.1kg,R1=1Ω
(2)金属杆ab运动的加速度为$\frac{1}{2}$gsinθ时,I′=$\frac{BLv′}{{R}_{总}}$
根据牛顿第二定律,得mgsinθ-BI′L=ma
代入得 mgsinθ-$\frac{{B}^{2}{L}^{2}v}{{R}_{1}R}({R}_{1}+R)$=$\frac{1}{2}$mgsinθ
代入数据,得到v′=0.5m/s
(3)当变阻箱R取1Ω时,根据图象得到vm=1m/s,则由题v=$\frac{{v}_{m}}{2}$=0.5m/s
定值电阻R1消耗的电功率为
P=$\frac{{E}^{2}}{{R}_{1}}$=$\frac{{B}^{2}{L}^{2}{v}^{2}}{{R}_{1}}$
代入数据得:P=0.0625W
答:(1)金属杆的质量m是0.1kg,定值电阻的阻值R1是1Ω.
(2)当变阻箱R取1Ω时,且金属杆ab运动的加速度为$\frac{1}{2}$gsinθ时,此时金属杆ab运动的速度是0.5m/s.
(3)当变阻箱R取1Ω时,且金属杆ab运动的速度为$\frac{{v}_{m}}{2}$时,定值电阻R1消耗的电功率是0.0625W.
点评 本题根据平衡条件和安培力公式得到$\frac{1}{{v}_{m}}$与$\frac{1}{R}$的关系式是解题的关键,结合数学知识即可求得有关量.

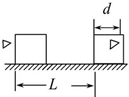 如图所示,木块静止在光滑水平桌面上,一子弹水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿桌面移动的距离为L,木块对子弹的平均阻力为Ff,那么在这一过程中不正确的是( )
如图所示,木块静止在光滑水平桌面上,一子弹水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿桌面移动的距离为L,木块对子弹的平均阻力为Ff,那么在这一过程中不正确的是( )| A. | 木块的动能增加量为FfL | B. | 子弹的动能减少量为Ff(L+d) | ||
| C. | 系统的机械能减少量为Ffd | D. | 系统的机械能减少量为Ff(L+d) |
| A. | 4:1 1:2 | B. | 4:1 2:1 | C. | 1:4 1:2 | D. | 1:4 2:1 |
 如图所示,理想变压器线圈匝数比n1:n2=1:2,分别接有相同的两只灯泡A和B,若在a、b间接正弦式交流电源,电源电压为U,则B灯两端电压为( )
如图所示,理想变压器线圈匝数比n1:n2=1:2,分别接有相同的两只灯泡A和B,若在a、b间接正弦式交流电源,电源电压为U,则B灯两端电压为( )| A. | 2U | B. | $\frac{2U}{3}$ | C. | 0.4U | D. | U |
| A. | 自由落体运动是初速度为零的匀加速直线运动 | |
| B. | 自由落体运动的末速度可以是零 | |
| C. | 自由落体运动在开始连续的三个1s末的速度之比是1:3:5 | |
| D. | 自由落体运动在开始连续的三个2s内的位移之比是1:4:9 |
 悬挂在O点的一根不可伸长的绝缘细线下端有一个质量为m、带电量为q的小球,若在空间加
悬挂在O点的一根不可伸长的绝缘细线下端有一个质量为m、带电量为q的小球,若在空间加 如图所示,PQ、MN为水平、平行放置的金属导轨相距1m,导体棒ab跨放在导轨上,棒的质量为m=0.2kg,棒的中点用轻绳经滑轮与物体相连,物体的质量M=0.3kg,棒与导轨的动摩擦因数为μ=0.5,设最大静摩擦力等于滑动摩擦力,匀强磁场的磁感应强度B=2T,方向竖直向下,为了使物体保持静止状态,可在棒中通入多大的电流?方向如何?(g取10m/s2)
如图所示,PQ、MN为水平、平行放置的金属导轨相距1m,导体棒ab跨放在导轨上,棒的质量为m=0.2kg,棒的中点用轻绳经滑轮与物体相连,物体的质量M=0.3kg,棒与导轨的动摩擦因数为μ=0.5,设最大静摩擦力等于滑动摩擦力,匀强磁场的磁感应强度B=2T,方向竖直向下,为了使物体保持静止状态,可在棒中通入多大的电流?方向如何?(g取10m/s2) 用等效代替法验证力的平行四边形定则的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳,图乙是白纸上根据实验结果画出的图.
用等效代替法验证力的平行四边形定则的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳,图乙是白纸上根据实验结果画出的图. 质量分别为5㎏和10㎏的物体A和B叠放在水平面上,如图设A、B间的最大静摩擦力为20N,B与水平面间的动摩擦因数μ=0.1,现用水平力F作用于B使AB一同加速运动,则力F满足条件:15N<F≤75N,若水平力F作用于A使AB一同加速运动,则力F满足条件:15N<F≤22.5N.(g=10m/s2)
质量分别为5㎏和10㎏的物体A和B叠放在水平面上,如图设A、B间的最大静摩擦力为20N,B与水平面间的动摩擦因数μ=0.1,现用水平力F作用于B使AB一同加速运动,则力F满足条件:15N<F≤75N,若水平力F作用于A使AB一同加速运动,则力F满足条件:15N<F≤22.5N.(g=10m/s2)