题目内容
如图所示，质量是m的小球带有正电荷，电量为q，小球中间有一孔套在足够长的绝缘细杆上．杆与水平方向成θ角，与球的动摩擦因数为μ，此装置放在沿水平方向磁感应强度为B的匀强磁场中．若从高处将小球无初速释放，求：小球下滑过程中加速度的最大值和运动速度的最大值．
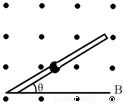
【答案】分析：小球受重力、垂直杆子向上的洛伦兹力，垂直杆子向上的弹力、摩擦力，当弹力等于零，摩擦力为零，此时加速度最大．当加速度为零时，小球的速度最大．
解答：解：当杆对小球支持力N=0时，加速度最大
mgsinθ=ma a=gsinθ
小球匀速运动时，运动速度最大mgsinθ=μN
mgcosθ+N=qvB
解得v=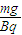
（
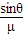+cosθ）
答：小球下滑过程中的最大加速度为gsinθ，最大速度为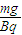
（
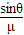+cosθ）．
点评：解决本题的关键理清小球的运动规律，知道摩擦力为零时，加速度最大，当加速度为零时，速度最大．
解答：解：当杆对小球支持力N=0时，加速度最大
mgsinθ=ma a=gsinθ
小球匀速运动时，运动速度最大mgsinθ=μN
mgcosθ+N=qvB
解得v=
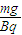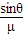（+cosθ）答：小球下滑过程中的最大加速度为gsinθ，最大速度为
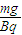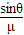（+cosθ）．点评：解决本题的关键理清小球的运动规律，知道摩擦力为零时，加速度最大，当加速度为零时，速度最大．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，质量是m的小球带有正电荷，电量为q，小球中间有一孔套在足够长的绝缘细杆上．杆与水平方向成θ角，与球的动摩擦因数为μ，此装置放在沿水平方向磁感应强度为B的匀强磁场中．若从高处将小球无初速释放，
（1）二者相对静止时共同速度为多少？
，一个质量为m的小滑块以初速度
从左端滑上木板，由于滑块与木板间的摩擦作用，木板也开始向右滑动，滑块滑到木板右端时二者恰好相对静止，求：
，一个质量为m的小滑块
以初速度
从左端滑上木板，由于滑块与木板间的摩擦作用，木板也开始向右滑动，滑块滑到木板右端时二者恰好相对静止，求：
