题目内容
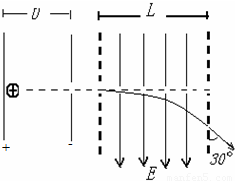
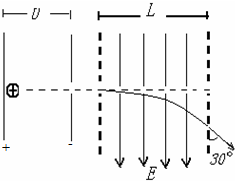 如图示,不计重力的带正电粒子在电容器中,由正极板静止释放.电容器两极板电势差为U,带电粒子电量为q,质量为m,粒子从右极板中心小孔射出后,垂直进入竖直向下的匀强电场,电场所在区域水平宽度为L,粒子穿出电场时速度方向与竖直方向夹角为30°,求:
如图示,不计重力的带正电粒子在电容器中,由正极板静止释放.电容器两极板电势差为U,带电粒子电量为q,质量为m,粒子从右极板中心小孔射出后,垂直进入竖直向下的匀强电场,电场所在区域水平宽度为L,粒子穿出电场时速度方向与竖直方向夹角为30°,求:(1)带电粒子射出电容器的速度
(2)带电粒子在竖直向下的匀强电场中运动的时间
(3)竖直向下的匀强电场的电场强度大小.
分析:带电粒子在加速电场中做匀加速直线运动,可以用动能定理解出速度,进入偏转电场做类平抛运动,结合平抛运动规律解题:水平方向匀速直线运动,竖直方向初速度为零的匀加速直线运动.
解答:解:(1)带电粒子在电容器中加速,出电容器时速度为V,此过程只有电场力做功,
由动能定理:qU=
mv2-0,
解得:v=
(2)带电粒子垂直进入匀强电场做类平抛运动
水平方向:x=L=vt
得:t=L
(3)粒子射出电场时与竖直方向300夹角,
cot30°=
=
=
解得:E=
答:(1)带电粒子射出电容器的速度为
.
(2)带电粒子在竖直向下的匀强电场中运动的时间为L
.
(3)竖直向下的匀强电场的电场强度大小为
.
由动能定理:qU=
| 1 |
| 2 |
解得:v=
|
(2)带电粒子垂直进入匀强电场做类平抛运动
水平方向:x=L=vt
得:t=L
|
(3)粒子射出电场时与竖直方向300夹角,
cot30°=
| Vy |
| Vx |
| at |
| V |
| qEL |
| mv2 |
解得:E=
2
| ||
| L |
答:(1)带电粒子射出电容器的速度为
|
(2)带电粒子在竖直向下的匀强电场中运动的时间为L
|
(3)竖直向下的匀强电场的电场强度大小为
2
| ||
| L |
点评:注意类平抛运动过程水平方向的运动与竖直方向的运动具有等时性,然后分别应用匀速运动规律和初速度为零匀加速直线运动规律解题.

练习册系列答案
相关题目
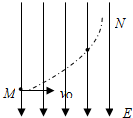 如图所示,在竖直向下的匀强电场中,一个带电粒子以初速度v0水平射入电场中(不计重力),在电场力作用下作图示的曲线运动,从M到N的过程中,下列说法中正确的是( )
如图所示,在竖直向下的匀强电场中,一个带电粒子以初速度v0水平射入电场中(不计重力),在电场力作用下作图示的曲线运动,从M到N的过程中,下列说法中正确的是( )| A、粒子一定带负电 | B、粒子的速度越来越小 | C、粒子的加速度越来越大 | D、电场力对粒子做负功 |
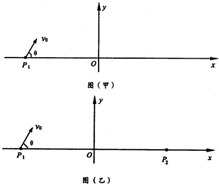 如图所示,质量均为m、电荷量均为q的带负电的一簇粒子从P1(-a,b)点以相同的速率v0在:xoy平面内朝x轴上方的各个方向射出(即0<θ≤π),不计重力及粒子间的相互作用,且已知a足够大.
如图所示,质量均为m、电荷量均为q的带负电的一簇粒子从P1(-a,b)点以相同的速率v0在:xoy平面内朝x轴上方的各个方向射出(即0<θ≤π),不计重力及粒子间的相互作用,且已知a足够大.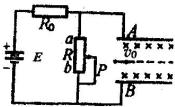 如图所示,电源电动势为E,内阻忽略不计,滑动变阻器的滑片P置于中点:两平行极板间有垂直纸面的匀强磁场,一带正电的粒子以速度υo正好水平向右匀速穿过两板 (不计重力).以下说法错误的是( )
如图所示,电源电动势为E,内阻忽略不计,滑动变阻器的滑片P置于中点:两平行极板间有垂直纸面的匀强磁场,一带正电的粒子以速度υo正好水平向右匀速穿过两板 (不计重力).以下说法错误的是( )