题目内容
18.物体静止在光滑水平面上,先对物体施加一水平向右的恒力F1,经过时间t后撤去F1,立即再对它施加一个水平向左的恒力F2,又经过时间4t物体回到出发点,此时物体的动能为50J,求:(1)恒力F1与恒力F2的比值
(2)恒力F1对物体做的功W1和恒力F2对物体做的功W2各为多少.
分析 (1)根据平均速度公式可求得位移表达式,再根据位移关系可明确速度关系;再由动量定理可求得两力的大小之比;
(2)全程中两力做功的位移相等,则可求得两力做功之比;再根据动能定理可求得两力做功之比.
解答 解:(1)设ts后的速度为v1;回到出发点时的速度为v2;
则由平均速度公式可得:
x1=$\frac{{v}_{1}}{2}t$;
x2=$\frac{{v}_{1}+{v}_{2}}{2}$t;
根据题意可知,x1=-x2
联立解得:v1=-0.8v2;
对两过程由动量定理可知:
F1t=mv1;
F2×4t=mv2-mv1
解得:$\frac{{F}_{1}}{{F}_{2}}$=$\frac{16}{9}$;
(2)对全过程分析可知:两力作用的位移大小相等,设F1做功为W1,F2做功为W2;
$\frac{{W}_{1}}{{W}_{2}}$=$\frac{{F}_{1}}{{F}_{2}}$=$\frac{16}{9}$;由动能定理可知,
W1+W2=$\frac{1}{2}$mv2;
联立解得,W1=32J;W2=18J;
答:(1)恒力F1与恒力F2的比值为16:9;
(2)恒力F1对物体做的功W1和恒力F2对物体做的功W2各为32J和18J.
点评 本题考查动能定理及动量定理的应用,要注意明确两过程中位移大小相等,方向相反;注意正确利用平均速度公式及动量定理和动能定理求解;本题中求力时也可以根据牛顿第二定律求解.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
9. 如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )
如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )
 如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )
如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为v0)( )| A. | 若把斜面AB变成曲面AEB,物体沿此曲面上升仍能到达B点 | |
| B. | 若把斜面CB部分截去,物体冲过C点后上升的最大高度仍为h | |
| C. | 若把斜面从C点以上部分弯成与C点相切的圆弧状,物体上升的最大高度有可能仍为h | |
| D. | 若把斜面弯成圆弧形D,物体仍沿圆弧升高h |
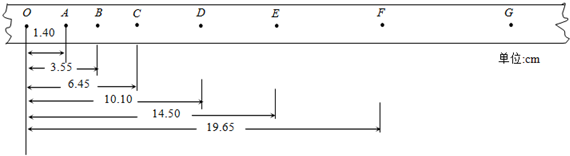
6.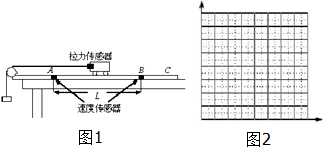 某实验小组利用力传感器和光电门传感器探究“动能定理”,将力传感器固定在小车上,用不可伸长的细线通过一个定滑轮与重物G相连,力传感器记录小车受到拉力的大小,在水平轨道上A、B两点各固定一个光电门传感器,用于测量小车的速度v1和v2,如图1所示,在小车上放置砝码来改变水上车质量,用不同的重物G来改变拉力的大小,摩擦力不计.
某实验小组利用力传感器和光电门传感器探究“动能定理”,将力传感器固定在小车上,用不可伸长的细线通过一个定滑轮与重物G相连,力传感器记录小车受到拉力的大小,在水平轨道上A、B两点各固定一个光电门传感器,用于测量小车的速度v1和v2,如图1所示,在小车上放置砝码来改变水上车质量,用不同的重物G来改变拉力的大小,摩擦力不计.
(1)实验主要步骤如下:
①测量小车和拉力传感器的总质量M1,把细线的一端固定在力传感器上,另一端通过定滑轮与重物G相连,正确连接所需电路;
②将小车停在点C(点C在光电门B的右侧),由静止开始释放小车,小车在细线拉动下运动,除了光电门传感器测量速度和力传感器测量速度和力传感器测量拉力的数据以外,还应该记录的物理量为两光电门间的距离(或AB间距离).
③改变小车的质量或重物的质量,重复②的操作.
(2)下面表格中M是M1与小车中砝码质量之和,(△E为动能变化量),F是拉力传感器的拉力,W是F在A、B间所做的功,表中的△E2=0.600,W2=0.610(数据保留三位有效数字).
(3)根据表中的数据,请在图2坐标上作出△E-W图线.
 某实验小组利用力传感器和光电门传感器探究“动能定理”,将力传感器固定在小车上,用不可伸长的细线通过一个定滑轮与重物G相连,力传感器记录小车受到拉力的大小,在水平轨道上A、B两点各固定一个光电门传感器,用于测量小车的速度v1和v2,如图1所示,在小车上放置砝码来改变水上车质量,用不同的重物G来改变拉力的大小,摩擦力不计.
某实验小组利用力传感器和光电门传感器探究“动能定理”,将力传感器固定在小车上,用不可伸长的细线通过一个定滑轮与重物G相连,力传感器记录小车受到拉力的大小,在水平轨道上A、B两点各固定一个光电门传感器,用于测量小车的速度v1和v2,如图1所示,在小车上放置砝码来改变水上车质量,用不同的重物G来改变拉力的大小,摩擦力不计.(1)实验主要步骤如下:
①测量小车和拉力传感器的总质量M1,把细线的一端固定在力传感器上,另一端通过定滑轮与重物G相连,正确连接所需电路;
②将小车停在点C(点C在光电门B的右侧),由静止开始释放小车,小车在细线拉动下运动,除了光电门传感器测量速度和力传感器测量速度和力传感器测量拉力的数据以外,还应该记录的物理量为两光电门间的距离(或AB间距离).
③改变小车的质量或重物的质量,重复②的操作.
(2)下面表格中M是M1与小车中砝码质量之和,(△E为动能变化量),F是拉力传感器的拉力,W是F在A、B间所做的功,表中的△E2=0.600,W2=0.610(数据保留三位有效数字).
| 次数 | M/kg | |v22-v12|/m2•s-2 | △E/J | F/N | W/J |
| 1 | 0.500 | 0.760 | 0.190 | 0.400 | 0.200 |
| 2 | 0.500 | 1.65 | 0.413 | 0.840 | 0.420 |
| 3 | 0.500 | 2.40 | △E3 | 1.22 | W3 |
| 4 | 1.00 | 2.40 | 1.20 | 2.42 | 1.21 |
10.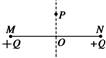 如图所示,M、N为两个固定的等量同种正电荷,在其连线的中垂线上的P点放一个静止的负电荷(重力不计),下列说法中正确的是( )
如图所示,M、N为两个固定的等量同种正电荷,在其连线的中垂线上的P点放一个静止的负电荷(重力不计),下列说法中正确的是( )
 如图所示,M、N为两个固定的等量同种正电荷,在其连线的中垂线上的P点放一个静止的负电荷(重力不计),下列说法中正确的是( )
如图所示,M、N为两个固定的等量同种正电荷,在其连线的中垂线上的P点放一个静止的负电荷(重力不计),下列说法中正确的是( )| A. | 从P到O,可能加速度越来越小,速度越来越大 | |
| B. | 从P到O,可能加速度先变大,再变小,速度越来越大 | |
| C. | 越过O点后,电势能越来越大,直到速度为零 | |
| D. | 越过O点后,动能越来越大,直到电势能为零 |
7. 如图所示是某空间部分电场线分布图,在电场中取一点O,以O为圆心的圆周上M、Q、N三个点,连线MON与直电场线重合,连线OQ垂直于MON,下列说法正确的是( )
如图所示是某空间部分电场线分布图,在电场中取一点O,以O为圆心的圆周上M、Q、N三个点,连线MON与直电场线重合,连线OQ垂直于MON,下列说法正确的是( )
 如图所示是某空间部分电场线分布图,在电场中取一点O,以O为圆心的圆周上M、Q、N三个点,连线MON与直电场线重合,连线OQ垂直于MON,下列说法正确的是( )
如图所示是某空间部分电场线分布图,在电场中取一点O,以O为圆心的圆周上M、Q、N三个点,连线MON与直电场线重合,连线OQ垂直于MON,下列说法正确的是( )| A. | M点的场强大于N点的场强 | |
| B. | O点的电势等于Q点的电势 | |
| C. | 将一负点电荷由M点移到Q点,电荷的电势能增加 | |
| D. | 一正点电荷从M运动到O点电场力做的功大于从O点到N点电场力做的功 |
8. 如图所示为交流发电机原理图,αbcd为交流发电机的矩形线圈,其面积为S,匝数为n,线圈电阻为r,外电阻为R0,线圈在磁感应强度为B的匀强磁场中绕垂直于磁场的转轴OO′顺时针匀速转动,角速度为ω.若图中的电压表、电流表均为理想交流电表,则下列说法正确的是( )
如图所示为交流发电机原理图,αbcd为交流发电机的矩形线圈,其面积为S,匝数为n,线圈电阻为r,外电阻为R0,线圈在磁感应强度为B的匀强磁场中绕垂直于磁场的转轴OO′顺时针匀速转动,角速度为ω.若图中的电压表、电流表均为理想交流电表,则下列说法正确的是( )
 如图所示为交流发电机原理图,αbcd为交流发电机的矩形线圈,其面积为S,匝数为n,线圈电阻为r,外电阻为R0,线圈在磁感应强度为B的匀强磁场中绕垂直于磁场的转轴OO′顺时针匀速转动,角速度为ω.若图中的电压表、电流表均为理想交流电表,则下列说法正确的是( )
如图所示为交流发电机原理图,αbcd为交流发电机的矩形线圈,其面积为S,匝数为n,线圈电阻为r,外电阻为R0,线圈在磁感应强度为B的匀强磁场中绕垂直于磁场的转轴OO′顺时针匀速转动,角速度为ω.若图中的电压表、电流表均为理想交流电表,则下列说法正确的是( )| A. | 此交流发电机产生的感应电动势的最大值为Em=$\sqrt{2}$nBSω | |
| B. | 若从图示位置开始计时,则感应电动势随时间变化的函数表达式为e=nBSωcosωt | |
| C. | 电流表的示数为I=$\frac{nBSω}{(r+R)}$ | |
| D. | 此交流发电机的输出功率P=$\frac{{n}^{2}{B}^{2}{S}^{2}{ω}^{2}R}{2(R+r)^{2}}$ |