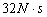题目内容
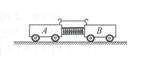
如图所示,在水平光滑桌面上有两辆静止的小车A和B,质量之比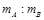 =3∶1。将两车用细线拴在一起,中间有一被压缩的弹簧。烧断细线后至弹簧恢复原长前的某一时刻,两辆小车的( )
=3∶1。将两车用细线拴在一起,中间有一被压缩的弹簧。烧断细线后至弹簧恢复原长前的某一时刻,两辆小车的( )
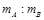 =3∶1。将两车用细线拴在一起,中间有一被压缩的弹簧。烧断细线后至弹簧恢复原长前的某一时刻,两辆小车的( )
=3∶1。将两车用细线拴在一起,中间有一被压缩的弹簧。烧断细线后至弹簧恢复原长前的某一时刻,两辆小车的( )
A.加速度大小之比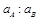 =1∶1 =1∶1 |
B.速度大小之比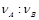 =1∶3 =1∶3 |
C.动能之比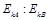 =1∶9 =1∶9 |
D.动量大小之比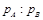 =1∶3 =1∶3 |
B
分析:先根据动量守恒守恒求出脱离弹簧后两车的速度之比,根据动能、动量的表达式求出动能及动量之比,根据弹簧对两车做功等于车动能的变化量求出弹簧对两车做功之比.
解:根据牛顿第三定律可知两车受力等大反向
根据牛顿第二定律a=F/m
可知加速度大小之比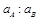 =
=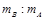 =1∶3
=1∶3
故A错误
在两车刚好脱离弹簧时运用动量守恒得:
pA+pB=0,两车的动量大小之比pA:pB=1:1故D错误;
3mvA+mvB=0
得:vA=-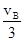
两车速度大小之比为: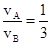 ,故B正确;
,故B正确;
两车的动能之比EkA:EkB=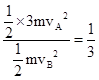 ,故C错误;
,故C错误;
故选B.
解:根据牛顿第三定律可知两车受力等大反向
根据牛顿第二定律a=F/m
可知加速度大小之比
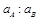 =
=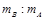 =1∶3
=1∶3故A错误
在两车刚好脱离弹簧时运用动量守恒得:
pA+pB=0,两车的动量大小之比pA:pB=1:1故D错误;
3mvA+mvB=0
得:vA=-
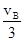
两车速度大小之比为:
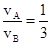 ,故B正确;
,故B正确;两车的动能之比EkA:EkB=
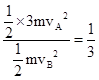 ,故C错误;
,故C错误;故选B.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
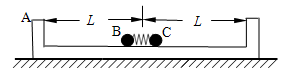
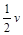 ,方向相反.则两小球质量之比m1:m2和碰撞前后动能变化量之比
,方向相反.则两小球质量之比m1:m2和碰撞前后动能变化量之比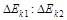 为
为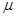 ,则在足够长的时间内( )
,则在足够长的时间内( )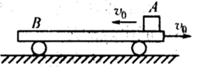
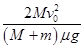
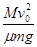
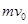
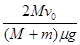
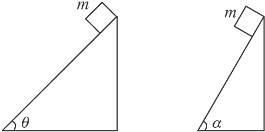
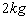 的质点从静止开始沿某一方向做匀加速直线运动,它的动量
的质点从静止开始沿某一方向做匀加速直线运动,它的动量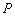 随位移变化的关系式为
随位移变化的关系式为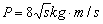 ,则此质点( )
,则此质点( )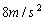
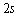 内受到的冲量为
内受到的冲量为