如图所示.光滑水平直轨道上有三个滑块A.B.C.质量分别为mA＝mC＝2m.mB＝m.A.B用细绳连接.中间有一压缩的轻弹簧．开始时A.B以共同速度v0运动.C静止．某时刻细绳突然断开.A.B被弹开.然后B又与C发生碰撞并粘在一起.最终三滑块速度恰好相同．求B与C碰撞前B的速度．题目和参考答案——青夏教育精英家教网—

题目内容

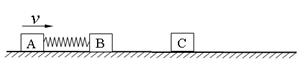
如图所示，光滑水平直轨道上有三个滑块A、B、C，质量分别为m_A＝m_C＝2m，m_B＝m，A、B用细绳连接，中间有一压缩的轻弹簧（弹簧与滑块不拴接）．开始时A、B以共同速度v₀运动，C静止．某时刻细绳突然断开，A、B被弹开，然后B又与C发生碰撞并粘在一起，最终三滑块速度恰好相同．求B与C碰撞前B的速度．

解析试题分析：设共同速度为v，球A与B分开后，B的速度为v_B，由动量守恒定律（m_A＋m_B）v₀＝m_Av＋m_Bv_B①
m_Bv_B＝（m_B＋m_C）v②
联立①②式，得B与C碰撞前B的速度v_B＝.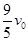
考点：动量守恒定律

练习册系列答案

相关题目

如图所示，长为L绝缘轻杆在水平向右的匀强电场中，杆与电场线垂直，杆两端固定带电小球A和B，初始时处于图中实线位置。现将轻杆向右平移2L，然后以球B为轴在纸面内顺时针转动90°到图中虚线位置，杆与电场线平行，在实线位置和虚线位置，A、B两球电势能之和相同。不考虑带电两球之间的相互作用。则

A.A球所带电荷量绝对值比B球的大
B.A球所带电荷量绝对值比B球的小
C.从实线位置到虚线位置的过程中，电场力对A球一定做正功
D.从实线位置到虚线位置的过程中，电场力对B球可能做正功

如图所示，物体在一个沿斜面的拉力F的作用下，以一定的初速度沿倾角为30°的斜面向上做匀减速运动，加速度的大小为a=3m/s²，物体在沿斜面向上的运动过程中，以下法正确的有

A．拉力F比摩擦力小

B．物体的机械能减少

C．物体动能的减少等于F与摩擦力所做功的总功

D．F与摩擦力所做功的总功等于物体机械能的增加量

如图所示，质量为m、电荷量为q的带电粒子，以初速度v₀垂直射入场强为E方向竖直向下的匀强电场中，该粒子在电场中的经历时间_____后，其即时速度的方向与初速度方向成30º角。在这过程中粒子的电势能增量为_______。（不计重力）

（12分）如图所示，质量m₁＝0.1 kg，电阻R₁＝0.3 Ω，长度l＝0.4 m的导体棒ab横放在U形金属框架上．框架质量m₂＝0.2 kg，放在绝缘水平面上，与水平面间的动摩擦因数μ＝0.2. 相距0.4 m的MM′、NN′相互平行，电阻不计且足够长．电阻R₂＝0.1Ω的MN垂直于MM′.整个装置处于竖直向上的匀强磁场中，磁感应强度B＝0.5 T．垂直于ab施加F＝2 N的水平恒力，ab从静止开始无摩擦地运动，始终与MM′、NN′保持良好接触．当ab运动到某处时，框架开始运动．设框架与水平面间最大静摩擦力等于滑动摩擦力，g取10 m/s².

(1)求框架开始运动时ab速度v的大小；
(2)从ab开始运动到框架开始运动的过程中，MN上产生的热量Q＝0.1 J，求该过程ab位移x的大小．

两物块A、B用轻弹簧相连，质量均为m="2" kg，初始时弹簧处于原长，A、B两物块都以v＝6 m／s的速度在光滑的水平地面上运动，质量M="4" kg的物块C静止在前方，如图所示。B与C碰撞后二者会粘在一起运动。求在以后的运动中：

（1）当弹簧的弹性势能最大时，物块A的速度v₁为多大?
（2）系统中弹性势能的最大值E_P是多少?

（19分）如图所示，正方形单匝均匀线框abcd边长L=0.4m，每边电阻相等，总电阻R=0.5Ω。一根足够长的绝缘轻质细线跨过两个轻质光滑定滑轮，一端连接正方形线框，另一端连接绝缘物体P，物体P放在一个光滑的足够长的固定斜面上，斜面倾角θ=30°，斜面上方的细线与斜面平行。在正方形线框正下方有一有界的匀强磁场，上边界I和下边界II都水平，两边界之间距离也是L=0.4m。磁场方向水平且垂直纸面向里，磁感应强度大小B=0.5T。现让正方形线框的cd边距上边界I的正上方高度h=0.9m的位置由静止释放，且线框在运动过程中始终与磁场垂直，cd边始终保持水平，物体P始终在斜面上运动，线框刚好能以v=3m/s的速度进入并匀速通过磁场区域。释放前细线绷紧，重力加速度 g=10m/s²，不计空气阻力。

(1) 线框的cd边在匀强磁场中运动的过程中，c、d 间的电压是多大？
(2) 线框的质量m₁和物体P的质量m₂分别是多大？
(3) 在cd边刚进入磁场时，给线框施加一个竖直向下的拉力F使线框以进入磁场前的加速度匀加速通过磁场区域，在此过程中，力F做功W =0.23J，求正方形线框cd边产生的焦耳热是多少？

（12分）如图所示为某娱乐场的一种游戏装置的滑道示意图，其中AB为曲面滑道，BC为长28m水平滑道，动摩擦因数为0.2；水平滑道BC与半径为10m的四分之一圆弧滑道CD相切，DE为水池的水平面，水池足够深，以确保人落水后的安全。某人坐滑车从坡顶的A点由静止滑下，经过高度差为20m的B点时的速度为16 m/s，最后落在水面上。人和滑车的质量共为70kg，将人和滑车作为质点处理，g取l0rn/s²。问：

（1）从A到B的过程中，人的机械能是否守恒，
（2）到达C点时的速度为多少？
（3）落水点与C点的水平距离。

（8分）把带电荷量2×10^-8 C的正点电荷从无限远处移到电场中的A点，要克服电场力做功8×10^-6 J，若把该电荷从无限远处移到电场中的B点，需克服电场力做功2×10^-6 J，取无限远处电势为零.求：
(1)A点的电势.
(2)A、B两点的电势差.
(3)若把2×10^-5C的负电荷由A点移动到B点，电场力做的功.

试题分类