题目内容
4.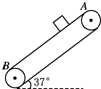 如图所示,传送带与地面倾角θ=37°,从A到B长度为16m,传送带以10m/s的速度转动.在传送带上端A处由静止轻放上一个质量为0.5kg的小物体,它与传送带之间的动摩擦因数为0.5.则当皮带轮处于下列两种情况时,求物体从A运动到B所用时间.(sin 37°=0.6,cos 37°=0.8,g取10m/s2)
如图所示,传送带与地面倾角θ=37°,从A到B长度为16m,传送带以10m/s的速度转动.在传送带上端A处由静止轻放上一个质量为0.5kg的小物体,它与传送带之间的动摩擦因数为0.5.则当皮带轮处于下列两种情况时,求物体从A运动到B所用时间.(sin 37°=0.6,cos 37°=0.8,g取10m/s2)(1)轮子沿顺时针方向转动;
(2)轮子沿逆时针方向转动.
分析 (1)轮子沿顺时针方向转动时,传送带作用于小物体的摩擦力沿传送带向上,根据牛顿第二定律求出物体的加速度,结合运动学公式求出速度达到传送带速度时的时间和位移,由于重力沿斜面方向的分力大于滑动摩擦力,速度相等后,滑动摩擦力沿斜面向上,结合位移时间公式求出剩余段匀加速运动的时间,从而得出物体从A运动到B的时间
(2)物体刚放上传送带,摩擦力的方向沿传送带向下,根据牛顿第二定律求出物体的加速度,结合运动学公式求出速度达到传送带速度时的时间和位移,由于重力沿斜面方向的分力大于滑动摩擦力,速度相等后,滑动摩擦力沿斜面向上,根据牛顿第二定律求出物体的加速度,结合位移时间公式求出剩余段匀加速运动的时间,从而得出物体从A运动到B的时间
解答 解:(1)轮子沿顺时针方向转动时,传送带作用于小物体的摩擦力沿传送带向上,物体的受力情况如图所示.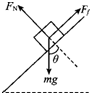
物体由静止加速,由牛顿第二定律可得
mgsin θ-μmgcos θ=ma1
解得:a1=2 m/s2,由于mgsinθ>μmgcosθ,物体受滑动摩擦力一直向上,
则物体从A端运动到B端的时间t=$\sqrt{\frac{2L}{{a}_{1}}}$=4 s.
(2)轮子沿逆时针方向转动时,传送带作用于小物体的摩擦力沿传送带向下,物体的受力情况如图所示.
物体由静止加速,由牛顿第二定律得
mgsin θ+μmgcos θ=ma2
解得:a2=10 m/s2
物体加速到与传送带速度相同需要的时间为
t1=$\frac{v}{a2}$=$\frac{10}{10}$ s=1 s
物体加速到与传送带速度相同时发生的位移为
s=$\frac{1}{2}$a2t${\;}_{1}^{2}$=$\frac{1}{2}$×10×12 m=5 m
由于μ<tan θ(μ=0.5,tan θ=0.75),物体在重力作用下将继续加速运动,物体的速度大于传送带的速度,传送带给物体的摩擦力沿传送带向上,物体加速度为
a3=2 m/s2
设后一阶段物体滑至底端所用时间为t2,由运动学公式有
L-s=vt2+$\frac{1}{2}$a3t${\;}_{2}^{2}$
解得t2=1 s
可知物体从A运动到B所用时间t′=t1+t2=2 s.
答:(1)轮子沿顺时针方向转动用时4 s;
(2)轮子沿逆时针方向转动用时2s
点评 解决本题的关键知道物体在传送带上的运动规律,结合运动学公式和牛顿第二定律综合求解,特别注意当物体速度达到与带同速时的摩擦力方向判断.

| A. | 1N | B. | 13N | C. | 2.5N | D. | 10N |
| A. | 库仑通过实验研究确定了点电荷之间的作用规律 | |
| B. | 欧姆首先实验得出电流通过导体时发热的规律 | |
| C. | 奥斯特发现通电导线周围存在磁场 | |
| D. | 安培首先提出了磁场对运动电荷有力的作用 |
| A. | 布朗运动是指悬浮固体颗粒的运动,反映了固体内部分子的无规则运动 | |
| B. | 温度一定时,水的饱和汽压也是一定的 | |
| C. | 第一类永动机违背了能量守恒定律,第二类永动机没有违背能量守恒定律,因此,随着科学技术的迅猛发展,第二类永动机是可以制成的 | |
| D. | 由阿伏加德罗常数、气体的摩尔质量和密度,可以估算出该种气体分子的大小 |
 图为湖边一倾角为30°的大坝横截面示意图,水面与大坝的交点为O.一人站在A点以速度v0沿水平方向扔一小石子,已知AO=40m,不计空气阻力,g取10m/s2.下列说法正确的是( )
图为湖边一倾角为30°的大坝横截面示意图,水面与大坝的交点为O.一人站在A点以速度v0沿水平方向扔一小石子,已知AO=40m,不计空气阻力,g取10m/s2.下列说法正确的是( )| A. | 若v0>18 m/s,则石子可以落入水中 | |
| B. | 若v0<20 m/s,则石子不能落入水中 | |
| C. | 若石子能落入水中,则v0越大,落水时速度方向与水平面的夹角越小 | |
| D. | 若石子不能落入水中,则v0越大,落到大坝上时速度方向与大坝的夹角越大 |
 如图所示,重物B放在水平地面上,通过摩擦不计的滑轮用绳与A相连,在图中位置保持静止状态,当将物体B向右移动一段距离后,仍在地面上保持静止状态,则关于物体所受的力的大小的说法中正确的是( )
如图所示,重物B放在水平地面上,通过摩擦不计的滑轮用绳与A相连,在图中位置保持静止状态,当将物体B向右移动一段距离后,仍在地面上保持静止状态,则关于物体所受的力的大小的说法中正确的是( )| A. | 重力与绳的拉力大小保持不变 | B. | 压力与摩擦力变大 | ||
| C. | 动摩擦因数大时,摩擦力大 | D. | 物体受合外力大小不变 |

| A. | Ea<Eb | B. | Ea>Eb | C. | φa>φb | D. | Ea=Eb |
| A. | 大小为20N,方向向东 | B. | 大小为20N,方向向西 | ||
| C. | 大小为60N,方向向东 | D. | 大小为60N,方向向西 |
 某人站在一平台上,用长L=0.5m的轻细线拴一个小球,让它在竖直平面内以O点为圆心做圆周运动,当小球转与最高点A时,人突然撤手.经0.8S小球落地,落地点B与A点的水平距离BC=4m,(g=10m/s2)
某人站在一平台上,用长L=0.5m的轻细线拴一个小球,让它在竖直平面内以O点为圆心做圆周运动,当小球转与最高点A时,人突然撤手.经0.8S小球落地,落地点B与A点的水平距离BC=4m,(g=10m/s2)