题目内容
【题目】图1是电子束加工工件的示意图,电子枪产生热电子后被高压电源加速,经聚焦系统会聚成很细的电子束,打在工件上产生高压力和强能量,对工件进行加工。图2是电子加速系统,K是与金属板M距离很近的灯丝,电源EA给K加热可以产生初速度不计的热电子,N为金属网,M、N接在输出电压恒为U的高压电源EB上,M、N之间的电场近似为匀强电场。系统放置在真空环境中,通过控制系统排走工件上的多余电子,保证N与工件之间无电压。正常工作时,若单位时间内从K发出的电子数为n,经M、N之间的电场加速后大多数电子从金属网N的小孔射出,少部分电子打到金属网丝上被吸收,从而形成回路电流,电流表的示数稳定为I.已知电子的质量为m、电量大小为e,不计电子所受的重力和电子之间的相互作用。求:
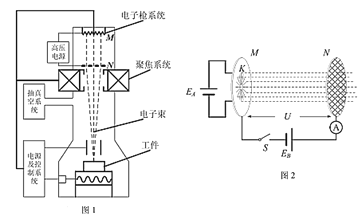
(1)单位时间内被金属网N吸收的电子数n′;若金属网N吸收电子的动能全部转化为内能,则其发热功率P为多少;
(2)电子在聚焦时运动方向改变很小,可认为垂直打到工件上时的速度与从N中射出时的速度相同,并假设电子打在工件上被工件全部吸收不反弹。求电子束打到工件表面时对工件的作用力F大小;并说明为增大这个作用力,可采取的合理可行的措施(至少说出两点方法);
(3)已知MN两板间的距离为d,设在两板之间与M相距x到x+△x的空间内(△x足够小)电子数为△N,求![]() 与x的关系式。
与x的关系式。
【答案】(1)IU(2)(n-![]() )
)![]() .见解析;(3)
.见解析;(3)![]() n
n![]()
【解析】
(1)电流表的示数稳定为I,在单位时间内打到金属网N上被吸收的电子数n′=![]() ;
;
设在金属网N上产生的热功率为P。
电子在MN间运动只有电场力做功,由动能定理可得:
Ue=![]() mv2;
mv2;
则P=n′![]() mv2;
mv2;
可得:P=IU;
(2)在△t时间内到达工件处的电子数为n2=(n-n′)△t;
那么,从作用效果来看,在△t时间内,有n2个电子与工件作用时速度由v减为0;
设电子受到工件的持续作用力大小为F,由动量定理可得:
-F△t=0-n2mv=-(n-n')mv△t;
所以,电子束打到工件表面时受到工件的作用力F=(n-n′)mv=(n-![]() )
)![]() ;
;
故由牛顿第三定律,电子对工件的作用力F′=F=(n-![]() )
)![]() ;
;
由作用力的表达式可知:增大这个作用力的办法:①增大电源EA辐射电子的功率。②增大EB电压U;③使金属丝变细且空格适当变大些,从而减少金属网N吸收的电子;
(3)设距M板x处电子速度为v,由动能定理得
![]() ex=
ex=![]()
设电子运动从x到△x的时间为△t.则△t=![]()
又因为n=![]() =△N
=△N![]()
所以![]() =
=![]() =n
=n![]()