题目内容
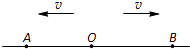（2012?虹口区二模）如图所示，A、B和O位于同一条直线上，波源O产生的横波沿该直线向左、右两侧传播，波速均为v．当波源起振后经过时间△t1，A点起振，再经过时间△t2，B点起振，此后A、B两点的振动方向始终相反，则下列说法中正确的是（ ）分析：振源O产生的横波沿直线向左右两侧传播，两列波关于波源具有对称性．简谐波传播过程中各质点的起振方向都与波源的起振方向相同．作出A点关于波源O点的对称点C，根据A、B两点的振动方向始终相反，分析A、B两点到振源O的距离之差与波长的关系．
解答：解：A、简谐波传播过程中各质点的起振方向都与波源的起振方向相同，A、B两点的起振方向相同，故A正确．
B、作出A点关于波源O点的对称点C，则有A、C两点的振动总是同步．A、B两点的振动方向始终相反，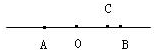
则C、B两点的振动方向始终相反，所以C、B间距离为半个波长，则A、B两点到振源O的距离之差为半波长的奇数倍，
xAB=（2n+1）
，△t2=（2n+1）
，T=
，n=0、1、2、3…，则最大周期T=2△t2，故B错误；
C、波长λ=vT=v
=
，n=0、1、2、3…，故C错误；
D、由B可知：则A、B两点到振源O的距离之差为半波长的奇数倍，xAB=（2n+1）
，n=0、1、2、3…，故D正确；
故选AD．
B、作出A点关于波源O点的对称点C，则有A、C两点的振动总是同步．A、B两点的振动方向始终相反，
则C、B两点的振动方向始终相反，所以C、B间距离为半个波长，则A、B两点到振源O的距离之差为半波长的奇数倍，
xAB=（2n+1）
| λ |
| 2 |
| T |
| 2 |
| △t2 | ||
n+
|
C、波长λ=vT=v
| △t2 | ||
n+
|
| 2v△t2 |
| 2n+1 |
D、由B可知：则A、B两点到振源O的距离之差为半波长的奇数倍，xAB=（2n+1）
| λ |
| 2 |
故选AD．
点评：本题波源产生两列左右对称的机械波，要抓住对称性．同一列波上振动情况总是相反的质点平衡位置距离最小等于半个波长．
练习册系列答案
相关题目
（2012?虹口区二模）如图所示，在柱形容器中装有部分水，容器上方有一可自由移动的活塞．容器水面浮有一个木块和一个一端封闭、开口向下的玻璃管，玻璃管中有部分空气，系统稳定时，玻璃管内空气柱在管外水面上方的长度为a，空气柱在管外水面下方的长度为b，水面上方木块的高度为c，水面下方木块的高度为d．现在活塞上方施加竖直向下、且缓缓增大的力F，使活塞下降一小段距离（未碰及玻璃管和木块），下列说法中正确的是（ ）
（2012?虹口区二模）在水平放置的光滑绝缘杆ab上，挂有两个金属环M和N，两环套在一个通电密绕长螺线管的中部，螺线管中部区域的管外磁场可以忽略．当变阻器的滑动头向左移动时，两环的运动情况是（ ）