题目内容
20.宇航员站在星球表面上某高处,沿水平方向抛出一小球,经过时间t小球落回星球表面,测得抛出点和落地点之间的距离为L.若抛出时的速度增大为原来的2倍,则抛出点到落地点之间的距离为$\sqrt{3}$L.已知两落地点在同一水平面上,该星球半径为R,已知引力常量为G,求该星球的质量及其表面的重力加速度大小.分析 运用平抛运动规律表示出抛出点与落地点之间的距离求解星球表面重力加速度.
忽略星球自转的影响,根据万有引力等于重力列出等式求解天体质量.
解答 解:设小球平抛初速度为V0,星球表面重力加速度为g,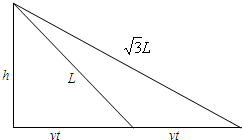
第一次平抛:(vt)2+($\frac{1}{2}$gt2)2=L2-------①
第二次平抛(2vt)2+($\frac{1}{2}$t2)2=($\sqrt{3}$L)2-------②
联立①和②解:g=$\frac{2\sqrt{3}L}{3{t}^{2}}$----------③
星球表面的物体受到的重力等于万有引力,即:G$\frac{Mm}{{R}^{2}}$=mg---------④
由③④解得:M=$\frac{2\sqrt{3}L{R}^{2}}{3G{t}^{2}}$;
答:该星球的质量为$\frac{2\sqrt{3}L{R}^{2}}{3G{t}^{2}}$,其表面的重力加速度大小为$\frac{2\sqrt{3}L}{3{t}^{2}}$.
点评 本题考查万有引力定律的应用,明确重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
11.在田径运动会投掷项目的比赛中,投掷链球、铅球、铁饼和标枪等都是把物体斜向上抛出的运动,如图所示,这些物体从被抛出到落地的过程中(不计空气阻力)( )


| A. | 物体的重力势能先增大后减小 | B. | 物体的动能先增大后减小 | ||
| C. | 物体的机械能先增大后减小 | D. | 物体的机械能保持不变 |
8.下面甲、乙两图中,一个是伏安法测电阻的实物连接图,另一个是用电流表和电压表测定电源电动势和内阻的实物连接图.

①测定电源电动势和内阻的实物连接图是图甲.按照该方法测量得到的电源电动势比真实值偏小,内阻比真实值偏小.(填“偏大”、“不变”或“偏小”).
表1
表2
②上面的表1和2是利用上面题中的实物图且当滑动变阻器的滑动触头逐渐向右移动时依次测得的实验数据表,其中与甲图对应的表格是丁表,在答题卡上画出其对应的电路图.

①测定电源电动势和内阻的实物连接图是图甲.按照该方法测量得到的电源电动势比真实值偏小,内阻比真实值偏小.(填“偏大”、“不变”或“偏小”).
表1
| V表读数/V | 0.81 | 1.21 | 1.70 | 1.81 | 2.51 |
| A表读数/A | 0.16 | 0.24 | 0.34 | 0.36 | 0.50 |
| V表读数/V | 1.37 | 1.32 | 1.24 | 1.18 | 1.05 |
| A表读数/A | 0.12 | 0.20 | 0.31 | 0.32 | 0.57 |
15.下列关于经典力学的说法中正确的是( )
| A. | 经典力学可以说明行星和卫星的运行轨道 | |
| B. | 经典力学适用于微观领域 | |
| C. | 经典力学只适用于微观、高速、强引力场 | |
| D. | 经典力学只适用于宏观、低速、弱引力场 |
5.关于核反应方程类型,下列说法正确的是( )
| A. | ${\;}_{11}^{24}$Na→${\;}_{12}^{24}$Mg+${\;}_{-1}^{0}$e 是α衰变 | |
| B. | ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{144}$Ba+${\;}_{36}^{89}$Kr+3${\;}_{0}^{1}$n 是裂变 | |
| C. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n 是裂变 | |
| D. | ${\;}_{86}^{222}$Rn→${\;}_{84}^{218}$Po+${\;}_{2}^{4}$He 是β衰变 |
12.如图甲所示,在水平向右的磁场中,竖直放置一个单匝金属圆线圈,线圈所围面积为0.1m2,线圈电阻为0.1Ω,磁场的磁感应强度大小B随时间t的变化规律如图乙所示,规定从左向右看顺时针方向为线圈中感应电流的正方向,则( )


| A. | 第2s内线圈有收缩的趋势 | B. | 第3s内线圈的发热功率最大 | ||
| C. | 第4s感应电流的方向为正方向 | D. | 0-5s内感应电流的最大值为0.1A |
10.一物体竖直向上抛出,从开始抛出到落回抛出点所经历的时间是t,上升的最大高度是h,所受空气阻力大小恒为F,则在时间t内( )
| A. | 物体动量的增量大于抛出时的动量 | |
| B. | 在上升过程中和下降过程中空气阻力对物体的冲量大小相等,方向相反 | |
| C. | 物体所受重力的冲量为零 | |
| D. | 物体机械能的减少量等于2Fh |
 如图,细绳的一端与质量m=0.3kg的小球相连,可绕过O点的水平轴自由转动.现在轨道的最低点a给小球以切线方向的速度v0=6m/s,使小球在竖直平面内做半径为R=0.5m的圆周运动.不考虑空气阻力,取g=10m/s2,求小球通过轨道最高点b时
如图,细绳的一端与质量m=0.3kg的小球相连,可绕过O点的水平轴自由转动.现在轨道的最低点a给小球以切线方向的速度v0=6m/s,使小球在竖直平面内做半径为R=0.5m的圆周运动.不考虑空气阻力,取g=10m/s2,求小球通过轨道最高点b时